DOI: 10.31038/GEMS.2022435

Abstract

Artefacts in the Williston Reservoir, British Columbia were collected and recorded by an archaeological firm over several years. While a large and extensive dataset of the locations of these artefacts was built up, several challenges to management and interpretation of the use of the landscape are presented. This study used the Variable Clumping Method (VCM) hierarchical clustering technique to detect clusters of artefacts for each object type. These detected clusters were then used for an object-type spatial correlation analysis, using Multivariate Local Indicators of Spatial Association (LISA). The results from LISA analysis included detection of significant global and local associations between several object-type pairs. For instance, strong spatial correlation was found between Scrapers and Points, which may suggest significant use areas, such as regularly used butchering sites or campsites. While it is not possible to draw a definitive conclusion of exactly what these relationships mean in terms of landscape use, they suggest a number of interesting hypotheses of possible uses of the area in the ancient time.

Keywords

Artefacts, Archaeological materials, Hierarchical clustering, Variable clumping method, LISA

Introduction

Archaeological data is intrinsically spatial in nature, and spatial analysis can often play a key role in interpreting the distribution of archaeological materials across a landscape. This approach is particularly useful in a situation where the artefacts are scattered across the site without stratigraphic relationships or known features to provide the context. In particular, spatial patterning among the artefacts and the behavioural interpretation across the site require rigorous intrasite spatial analysis and modelling so as to deduce the kind of activities that occurred at the site [1]. A range of intrasite spatial analytical techniques have been applied to date [2], but the treatment of the spatial patterns of the artefacts and other entities occasionally presents challenges at the point of interpretation as their spatial tendency is not always correctly recognised [3]. This is mainly due to the direct application of either (1) a non-spatial statistical approach whereby all observations are treated as spatially independent in nature and that spatial randomness is warranted as the base distribution behind the spatial arrangement of the artefacts, or (2) a spatial statistical approach with the understanding that spatial dependency exists among the intrasite spatial configuration of the artefacts but the spatial patterning is often sought with respect to a predetermined set of scales informed by the specific context of the site—in other words, the spatial statistical methods are usually applied with parameters set a priori, despite that contexts may not be always available. The spatial arrangement of the artefacts found or excavated at a site is likely to have spatial dependency among them, and the scale of activities (e.g. an individual engaging in a house task, or a community taking part in a social activity) will likely vary between the types of activities and the participants involved which are difficult to calibrate without stratigraphic narratives or known features that offer the context. The objective of this study is to identify spatial associations between different types of archaeological artefacts found across an excavation site and gain knowledge on the spatial configuration and the lifestyle of the ancient community that lived in this area. To overcome the challenges stated above, this study uses two types of spatial analytical methods that can extract the hierarchical spatial structure: (1) a local variant of a spatial autocorrelation method called Multivariate Local Indicators of Spatial Association (LISA) [4], and (2) a hierarchical cluster detection method called Variable Clumping Method (VCM) [5,6]. Clustering helps to simplify a large archaeological dataset to make spatial patterns easier to discern; but they need to be arranged at suitable scales with the recognition of the multi-scale across different levels of activities. Finding clusters in the distribution of the artefacts across multiple scales would provide more natural groupings for use in the subsequent analysis. Exploration of the spatial relationships between different types of artefacts through LISA could provide us with a clue to infer activities that took place in an ancient time and could greatly enhance our understanding on how the landscape was used at the time. The study focuses on artefacts retrieved from Williston Reservoir, British Columbia, Canada.

Literature Review

Spatial Analysis in Archaeology

Spatial analysis and GIS have been used in archaeology for years, as evidenced in a study by Kintigh and Ammerman (1982) [7] which highlights the usefulness of computer-based analysis, informed by expert interpretation, for identifying meaningful patterns in archaeological data. According to Carr (1984) [1], there are two levels of archaeological spatial analysis: inferential and operational. The goals of inferential analysis are to spatially delineate the activity areas as well as to identify the tool kits of artefact types. At the operational level, the focus is placed on identifying patterns in the spatial arrangement of different artefact types, including clustering, and relationships between different artefact types. In many cases, applying inferential analysis may not be suitable. Even where the spatial relationships between artefact types can be identified, Carr (1984) [1] cautions that these do not imply an activity area and that there may be a number of other possible explanations for the observed patterns. Dynamic processes, including human activities, occurring in both space and time, have contributed to the superimposition of materials to produce static patterns [8]. For instance, artefacts may have been found clustered due to intense human activity in that location in the past, but Wood and Johnson (1978) suggest it could also result from natural processes such as water transport and sorting, or recent human activity such as farming. Deriving the nature of these processes from the static patterns can therefore be extremely difficult. Nevertheless, spatial analysis has proven as an important step to understand the nature of the archaeological deposits. A number of methods for detecting patterns in the spatial distribution of archaeological deposits have been proposed in the past and applied by a number of studies [3]. For instance, Kintigh and Ammerman (1982) [7] used the k-means cluster detection technique to iteratively split and lump points in the dataset into a user-defined maximum number of clusters and, thereby, minimise the sum of the squares of the distances between each point and its cluster centre to find the optimal solution. More generally, Carr (1984) [1] refers to a number of methods used in intrasite archaeological contexts for determining presence of clustering as well as delimiting clusters in a point dataset. These include the Nearest Neighbour Analysis [9] used for determining presence of clustering; Whallon’s Radius Approach [10] for delimiting clusters using the frequency distribution of nearest neighbour distances between point observations; and conditional spatial patterning, a multi-scale method to test for spatial patterning in an archaeological dataset [8].Other applications of these methods vary in location, site type and the scale. For instance, in a cave site in Western Belize, artefacts scattered on different surfaces, including in niches and on ledges, were mapped and recorded in a GIS to analyse the spatial arrangement of the archaeological objects [11]. They adopted a clustering method, as some artefacts were found in multiple fragments in close proximity to one another and that the uses the individual object locations for analysis would have resulted in unequal weighting. A non-hierarchical method, k-means, was used to define natural groupings of objects in space, and the resultant clusters were analysed with regard to their association with cave features. Moyes’ (2002) [11] findings suggest that clustering and comparative analysis of the morphologic cave features could provide the context and the relative analytical units for use on a broader scale.

The examples above, however, are situations where the sites and the archaeological context are well defined. Many of these methods primarily deal with “more or less intact living surfaces” [12] that may not be applicable to other archaeological situations that lack an intact or a clear definition of the site. An example of such a situation is found in Australia; similar to the Williston Reservoir case, where the archaeology consists of open sites [13]. These open sites are extensive in area size, lack stratigraphy or clear boundaries, and contain few features [13]. In essence, it is a vast expanse of a surface scattered with primarily lithic artefacts. Site boundaries are difficult to determine in this type of landscape and, for the management purposes, arbitrary rules are often used to define boundaries that are not meaningful for analysis [13]. In these situations, a site-less analysis is required; i.e. the analysis is based on individual artefacts rather than sites [13]. As a result, the first step with open sites is to identify patterns in the spatial location of artefacts; after which, attempts can be made to interpret the patterns archaeologically. Holdaway et al. (1998) [13] address these concerns through geomorphological mapping of the landscape used for understanding the patterns of surface artefact density. This step determined that the depositional surfaces had lower artefact densities, which were excluded from the subsequent analysis to avoid bias in case undiscovered artefacts were buried under the sediments. Different buffer radii were used to look at different scales, and the resultant cluster patterns of individual artefact types were then used to identify assemblages and patterns between artefact types [13]. Other studies have also explored different methods for determining the associations between artefact types. These include a variety of statistical tests based on the number of artefact in partitioned units to determine patterns of aggregation and segregation between different artefact classes [14]. In this case, the definition of the unit shape and size may impact the results of the analysis. This is known as Modifiable Areal Unit Problem (MAUP) in spatial analysis [15,16]. Hietala and Stevens (1977) [14] therefore suggest changing the partition size to determine patterns for multiple partition options. Berry et al. (1980) [17] suggest the permutation test, which can use either grid-count values or point locations, and so can avoid the problems associated with defining a grid unit size. The permutation test uses as its test statistic the “average within-class distance” (Berry et al., 1980, p. 56) [17], and thus can test for significant associations between multiple classes. These methods detect global associations between artefact classes; i.e. they assess the overall density or the tendency of clustered-ness across the study area. However, as Premo (2004) [18] points out, being able to quantify the local spatial patterns (which enables us to identify the location, the extent and the intensity of each individual cluster) is important for the understanding and interpretation of archaeological material distributions. Methods for local spatial pattern detection used by Premo (2004) [18] include local Moran’s I and local G statistics, mainly for the purpose of detecting local spatial autocorrelation. These local statistics have a great potential for multiple archaeological applications, including that of multivariate analysis for identifying the association between artefact types or material types Premo (2004) [18].

Hierarchical Clustering Methods in Spatial Analysis

With the development of data collection technology such as Global Positioning Systems (GPS), remote sensing, and vast amount of spatial data is becoming increasingly available. Yet their interpretation is not always straightforward, and dealing with the data to extract meaningful information can be difficult at times. Exploratory spatial data analysis (ESDA) offers an important first step for deriving information from large spatial datasets [19]. Cluster analysis is a spatial extension of ESDA used across a broad range of disciplines, including crime analysis, disease analysis, and archaeology [6,7,20]. Cluster detection techniques for point datasets include techniques that simply determine the presence of clustering, such as nearest neighbour indices [21], as well as techniques that identify the individual points within a cluster [6]. Early clustering techniques include the Geographical Analysis Machine [22] for identifying hot spots or areas of high intensity; while more recent techniques are designed to identify which points belong to a particular cluster—some of these techniques can be classified further into partitioning, hierarchical, and graph-based techniques [21,23]. Partitioning methods, such as k-means, group all points in the dataset into a user-defined number of groups [21]. In addition to the disadvantage of having to specify a number of groups, which can lead to bias in the analysis, partitioning techniques are unable to identify cluster shapes that are not convex [24,25]. Hierarchical methods are typically either top-down or bottom-up; for top-down methods, points are either grouped into a single cluster, then that cluster split according to some function to create two clusters, those clusters further split, and so on [26]. Bottom-up methods, such as the nearest neighbour hierarchical clustering technique use some function to group the individual points into a number of clusters, then proceed to group the primary-level clusters into secondary-level clusters and so on, until there is a single cluster. One advantage of hierarchical methods is that the user does not specify how many clusters to generate; however, user-defined criterion are required to tell the software when to stop clustering, or to define the initial clustering criteria [21,24,26]. A limitation is that each level of clustering depends on the previous level. Graph-based techniques are those that compute a graph, where the points are vertices and edges are lines connecting pairs of points, with edge lengths representing the proximity of pairs of points [26]. The minimum spanning tree (MST) and Delaunay diagram are examples of graphs used in clustering algorithms. Some cluster methods falling into this category include AMOEBA [23], AUTOCLUST [26], and VCM [5]. AMOEBA and AUTOCLUST are similar techniques based on the Delaunay Diagram. AMOEBA uses the global mean and standard deviation of all edge lengths in the graph, compared to the local mean of all edges connected to a single point, to determine a tolerance value. Edge lengths exceeding this tolerance value are removed from the graph such that the remaining connected points form the clusters. The algorithm is then reiterated to generate sub-clusters from the primary clusters, and so on until no more edges are present in the graph, producing hierarchical clusters. AMOEBA detects clusters of different density, and also non-convex clusters [23]. AUTOCLUST is like AMOEBA, but it compares local mean and standard deviation of edge lengths for a point to the average local standard deviation of all points to determine the tolerance [26]. Like AMOEBA, it succeeds in identifying clusters of different density and arbitrary shape [26]. Other similar algorithms for finding clusters have been presented by various authors [25,27].

Variable clumping method (VCM) is a hierarchical and graph-based method that uses a minimum spanning tree (MST) as the graph of edges [5]. It detects “clumps” of points at varying distances by iterating through the ordered (by length) set of edges in the MST and using each length in turn as the radius of circles centered on the points, so that a set of points within connected circles constitute a clump [5]. The use of the variable radii enables detection of clumps at multiple scales. VCM also uses Monte Carlo simulation to determine which clumps at each radius are significant, and only includes these significant clumps in the final set [5,6]. All these clustering techniques offer many advantages but they also have limitations. Selecting an appropriate clustering technique requires defining the needs of the particular analysis to determine which limitations are acceptable. While there are hierarchical clustering approaches that would serve the needs of this analysis (e.g. AMOEBA, AUTOCLUST), they are mostly unavailable as a ready-to-use software package. CrimeStat is an exception, as a freely available software package that includes a nearest neighbour hierarchical clustering routine [21]. However, preliminary tests with this routine revealed several undesirable qualities such as the need to input parameters of the minimum number of points to include in the cluster, as well as the threshold distance [21], but these parameters may be difficult to estimate in a case where no context or the extent is available. Also, after running the clustering routine on a sample dataset (a subset of the Williston artefacts dataset), some of the member points within a cluster turned out to be closer to points in another cluster, which violates the primary goal of clustering as described above. Finally, each subsequent cluster level only clustered the clusters, so that outliers from the primary-level clustering remained isolated in the secondary-level clustering and so on. These attributes made it unsuitable for this study. To overcome these challenges, this study adopts the VCM approach. While it does require a user-defined parameter, this is only needed for specifying the number of hierarchical levels to generate, which is constrained by the amount of complexity the analysis can handle (with more levels, the complexity increases). As detailed in the discussion below, it ensures that the distances between points within a cluster are minimised, through the use of natural breaks, and that any point within the cluster is closer to other points within the cluster than it is to points outside the cluster. Also, each cluster level is based on the full set of points, so outliers from the first cluster level are incorporated into higher-order clusters.

Methodology

Study Area

The study area of Williston Reservoir is located in northern British Columbia, Canada. It was created by the construction of the WAC Bennett Dam in the late 1960s, and is one of the largest reservoirs in the world [28]. Reservoir operation over the last 50 years has led to the exposure of primarily unvegetated large expanses of “beach”, made up of fine silts, clays, gravels, or sand. This area was heavily used by the First Nations peoples throughout history, and physical evidence of this use remains on the landscape in the form of exposed surface lithic artefacts and other cultural remains [29,30]. Millennia Research Limited, an archaeological consulting firm, has conducted archaeological surveys of the inundation zone of Williston Reservoir annually since 2008. The surveyed area consists of discrete beaches, which are confined and delineated by the natural boundaries, usually in the forms of large creeks or rivers. Artefacts found during these surveys were recorded using handheld Global Positioning Systems (GPS) units, with an estimated average accuracy of ±5 m. The reservoir is composed of three main “reaches”, the northernmost of which is Finlay Reach, where the majority of the archaeological work has been done. Several of the core beaches of Finlay Reach (those that are most densely populated with artefacts) form the study area for this project (Figure 1). The archaeologically surveyed portion of these beaches totals over 68 km², in which over 6,000 artefacts have been recorded for 2009-2011 alone. The environment of the study area and the characteristics of the archaeological remains present some difficulties for the management of the archaeological resource. In British Columbia, archaeological resources are protected by law, and the provincial Archaeology Branch maintains a registry of the archaeological sites [31]. Thus, for management purposes, a site definition is required. In this environment, with vast areas covered by scatters of artefacts without clearly defined features, defining the boundaries of the archaeological site can be challenging. Furthermore, the management decisions for archaeological resources are often dependent on their significance. As highlighted by Glassow (1977) [32], significance can be difficult to define. This is even more so if the unit of analysis is unclear because the extent and the boundary of the archaeological site is ambiguous. Ideally, the unit of analysis should be extracted from non-arbitrary grouping of associated archaeological materials, yet identifying the categories for such grouping can be very difficult, because of the sheer volume of the Williston Reservoir artefact dataset, which makes visual identification of patterns impractical. There are other challenges such as the lack of stratigraphic context, defined landforms, or geomorphological features; as well as the lack of intact archaeological features. In addition, the landscape is not static, which means that new artefacts are discovered each year in areas that had been previously surveyed. All of these factors pose challenges for interpretation, analysis and management of this vast archaeological resource.

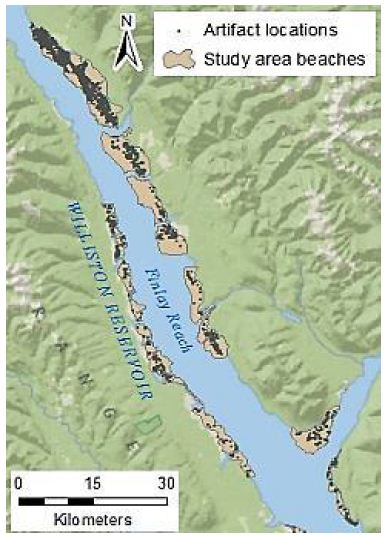
Figure 1: Study area beaches and artefact locations

Hierarchical Clustering

VCM is a spatial analytical method for detecting statistically significant multi-level clumps [5]. Circles of a variable-sized radius are drawn around each observed point, and any connected set of circles represents a clump. Clumps have some key properties including the clump radius (r) and the clump size (k), i.e. the number of connected circles. The “variable” part of VCM comes from varying the radius, so that the clumps identified at varying radii, and thus multi-scale clumps, are identified. The clumping state at a specific radius C(r) is defined by the number of clumps of size k at radius r, or N(k|r), so that C(r) = (N(2|r), N(3|r), … , N(n|r)) [6]. Note that a clump of size one is not considered a proper clump [5]. A minimum spanning tree (MST) represents the distances between points, using the property of edge length (l), so that at radius r, any points connected by an edge with length l ≤ r form a clump. Because clumps will appear even in a random distribution of points, VCM also conducts a significance analysis to determine which clumps are significant [5,6]. A radius interval and maximum radius are specified to define a set of radii for the analysis. The set of clumping states of the observed points for this set of radii is then determined. Next, 10,000 simulations, using randomly generated point distributions and finding the MST for these point distributions, provide a frequency distribution of clumping states for the set of radii. From this distribution, using a significance level (α) of α = 0.05, the critical number for each clump size at each radius is determined from this frequency distribution. The null hypothesis (H₀) states that the number of clumps of observed clump size k at a radius r will be less than or equal to the critical value for k and r. The results from the observed data are then compared to these critical values, and H₀ is rejected where the observed number of clumps of size k at radius r is greater than the critical value [5,6]. A clustering method such as VCM is based on the MST of the points in the dataset. However, this study used a classification method to limit the number of distances at which to generate clusters. Individual line segments of the MST were classified by length using a natural breaks classification, to determine the distance thresholds at which each cluster level was defined. Thus, the number of classes chosen defines the number of levels in the resulting hierarchy. Figure 2 illustrates this process. In Figure 2a, the MST line segments have been classified into five classes. Note that the “Class 5” line is dashed – this is to indicate that this class is not used as a cluster level, as it would include all of the points in the dataset. Figure 2b shows the convex hulls of the resultant clusters. The process is cumulative, so that “Cluster level 2” includes all points connected by “Class 1” as well as “Class 2” line lengths.

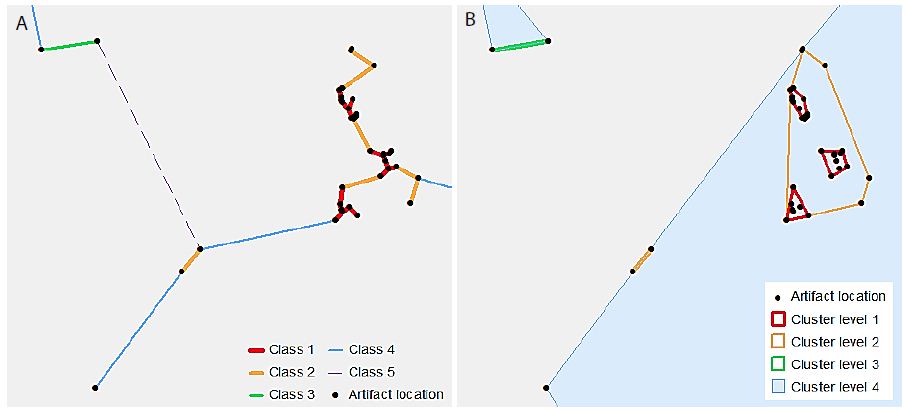
Figure 2: An illustrative example of hierarchical clusters; (a) classified MST lines connecting artefact point locations, (b) hierarchical clusters shown as convex hulls surrounding the original artefact point locations.

The specific methodology used for the dataset in this study was to first separate the overall artefact dataset into individual datasets by beach. This was done so that the resulting clusters would reflect the distribution of artefacts on a particular beach. Some of the beaches are densely populated with artefacts, while others are more sparsely populated. As the beaches are well-defined by major landforms (creeks and rivers), it is sensible that they should be treated individually. An MST was generated for each dataset, and then classified using the Natural Breaks classification method, which is based on Jenks’ optimisation method. In essence, this clustering problem is very similar to the choropleth mapping problem discussed by Jenks (1967) [33] in that, while it may seem ideal to present every data value, or in the case of hierarchical clustering, every possible cluster level, a limited number of classes must be used in order to be able to understand and interpret the data. In that case, it is desirable that each class should contain very similar values, so that the within-class deviation is minimised.

Step 1: Select all of the primary-level cluster lines (i.e. lines that have a length less than or equal to the Class 1 breakpoint).

Step 2: Buffer the selected lines.

Step 3: Dissolve any overlapping buffer polygons.

Step 4: Spatially join the original points layer to the buffer polygons, so that they are assigned the buffer polygon ID, which becomes the “Cluster 1 ID”.

Step 5: Generate convex hulls, grouping by Cluster 1 ID.

Step 6: Repeat above steps for each cluster level, such that the each successively higher cluster level includes all line lengths smaller than the break value (i.e., each cluster includes points from lower-order clusters).

The resulting datasets included a point dataset with all of the artefacts assigned an ID value for each cluster level, as well as convex hulls of all of the clusters at each level, and a size one standard deviation ellipse for each cluster at each level.

Bivariate Autocorrelation Analysis for Object Type Relationships

Bivariate local Moran’s statistical analysis [34] is often used for describing the spatial correlation between the spatial distribution patterns of two variables; i.e. it is a local method that identifies the actual locations where significant spatial dependency was observed between the two variables. GeoDa software [35] was used to perform a multivariate LISA analysis on pairs of object types in order to determine if any statistically significant relationships exist between them locally or globally. Anselin (1995) [4] defines a LISA as any statistic that indicates the degree and significance of spatial clustering of similar values around each observation. In addition, the sum of LISA statistics for a set of observations must be proportional to a global statistic [4]. GeoDa uses the Moran’s I statistic for LISA analysis. The global Moran’s I value is an indicator of overall clustering within the dataset, while the local Moran’s I value indicates the locations of clusters [36]. A significant local association may occur that is not globally significant, or there may be patterns occurring locally that are opposite to the global trend [4]. When applied as a multivariate test of spatial correlation, the statistic compares values for one variable at a location to values for a second variable at neighbouring locations. Values are “standardised such that the mean is zero and standard deviation equals one” [33]. The standardised values at each observation location are compared to the spatially lagged, standardised values at neighbouring locations to produce a global multivariate Moran’s I [34]. The contributions of individual observations to this global value are also calculated to determine local multivariate Moran’s I statistics. These values can then be compared to the values expected under a scenario of complete spatial randomness in order to determine the significance of the relationship between the two variables, both globally and locally [34]. This is done by calculating the Moran’s I for a large number of randomised permutations, in which one of the variables is kept static, while the other is randomly reallocated amongst the observations. Running several thousand random permutations produces an indicator of how extreme, and therefore how significant, the observed values are [4]. Thus, within the GeoDa multivariate LISA analysis, it is possible to obtain both global and local indicators of significant spatial association between two different variables. For each pair of variables a pseudo-significance level for the calculated local Moran’s I statistic was determined using 9,999 randomised permutations. The results, including the local Moran’s I value for each cluster with neighbours, the spatial association type, and the significance p-value for the association, were saved to a table.

The outcome of the significance test of LISA classifies individual cluster location into four different categories:

High-High

If the LISA statistic is statistically significant, takes a positive value, and the standardised count/value of object type A is positive, then both the object type A and the object type B are significantly high.

Low-Low

If the LISA statistic is statistically significant, takes a positive value, and the standardised count/value of object type A is negative, then both the object type A and the object type B are significantly low.

Low-High

If the LISA statistic is statistically significant, takes a negative value, and the standardised count/value of object type A is negative, then the object type A is low but the object type B is high.

High-Low

If the LISA statistic is statistically significant, takes a negative values, and the standardised count/value of object type A is positive, then the object type A is high but the object type B is low.

Analysis

In the analysis, a two-tier cluster levels were used for testing the spatial patterns of artefacts at different scales. The primary-level clusters were combined into a single dataset, and the secondary-level clusters were combined into another dataset. The object types that were used in the analysis are listed in Table 1. Some object type categories had very few members to the extent that they would not sustain robust analysis and were therefore excluded from the analysis. One very large category of object types, Flake Debitage, was also excluded because these items were often recorded only cursorily, making the data for this object type unreliable for use in this analysis.

Table 1: List of object types used in the analysis, with number of clusters for each object type

Object Type	#Level 1 Clusters	#Level 2 Clusters
Macroblade	74	61
Flake Tool	321	235
Impact Fractured Point	33	32
Cody Point (also included in point category)	30	29
Biface Preform	43	38
Scraper	379	211
Point (excludes impact fractured points)	227	167
Biface	119	106
Core	85	77
Microblade core	20	20
Microblade	35	32
Spall	71	63
Battered Biface	14	14
Hammer Stone	14	11
Alberta point (also included in point category)	6	5

GeoDa was used for generating a binary spatial weights matrix, in which a distance cut-off was applied to determine whether each cluster is considered a neighbour of another polygon. Clusters falling within the distance band are counted as neighbours in the analysis, and those falling outside the distance band are not considered [35]. GeoDa automatically calculates a distance that ensures that all clusters have at least one neighbour. However, the default distance turned out to be too large to provide archaeologically meaningful results, and it was adjusted through an exploratory process to calibrate it for localised analysis that also retains sufficient neighbours for most locations. Through this process, the primary-level clusters were set with the distance threshold of 250m, and the secondary-level clusters at 500 m. The resulting weights matrix for primary-level clusters had some isolated, neighbourless locations (Figure 3a). For the secondary-level clusters, every location had at least one neighbour (Figure 3b). This second level of analysis provides a more regional view of the relationships between object types, while the first level provides a more localised view.

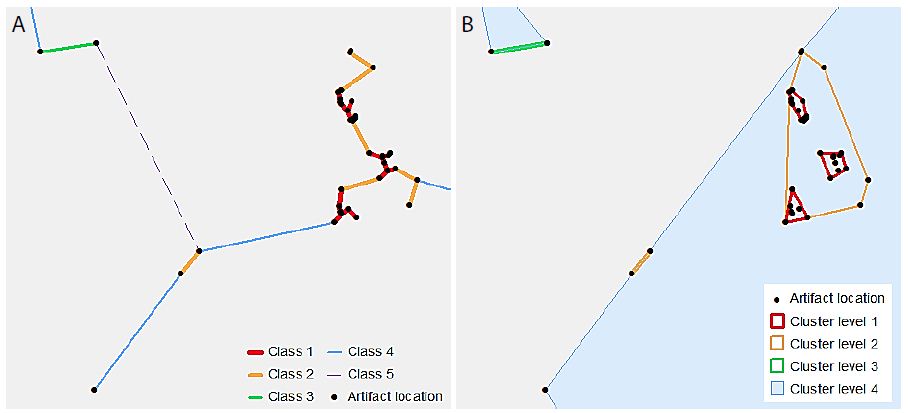
Figure 3: Detected artefacts clusters (a) distribution of primary-level clusters with the omission of the neighbourless clusters, (b) distribution of secondary-level clusters.

Of the 20 different relationships between object types tested at the first cluster level, three global significant relationships were discovered, and significant local associations were present in all of the comparisons. Amongst the statistically significant global patterns which emerged from the analysis was a positive correlation between Alberta Points and Macroblades. The negative correlations observed between Impact Fractured Points and Scrapers, and Impact Fractured Points and Flake Tools were statistically significant. The secondary-level cluster analysis did not result in many global significant associations; however, a positive correlation between Scraper object types and Point object types was significant. The secondary-cluster level results provide a more regional summary of the relationships between object types. None of the significant primary-level global associations were present as global associations for secondary-level clusters. Table 2 summaries the significant local relationships for primary-level clusters by their spatial association types, and Table 3 offers the same for secondary-level clusters. The association types are perhaps the most informative with regards to the nature of the relationships, as the actual Moran’s I value is not necessarily easy to interpret on its own.

Table 2: Significant results from primary-level multivariate local Moran’s I analysis

Core Variable	Spatially Lagged Variable	#Of Clusters with significant Relationship
		High-High	Low-Low	Low-High	High-Low
Battered Biface	Flake Tool	2	73	117	5
Battered Biface	Hammer Stone	1	511	78	12
Battered Biface	Scraper	1	54	150	3
Biface	Flake Tool	8	71	109	29
Biface Preform	Scraper	2	72	117	13
Macroblade	Microblade	1	227	165	43
Microblade	Microblade core	0	389	84	30
Core	Flake Tool	2	74	106	20
Flake Tool	Scraper	20	47	119	85
Point	Scraper	13	54	130	66
Alberta Point	Macroblade	3	104	178	2
Cody Point	Macroblade	3	100	182	21
Impact Fractured Point	Flake Tool	0	73	120	17
Impact Fractured Point	Point	1	163	117	14
Impact Fractured Point	Scraper	0	58	150	19
Scraper	Point	11	144	103	115
Scraper	Impact Fractured Point	3	182	58	240
Scraper	Flake Tool	17	66	95	82
Spall	Flake Tool	3	70	117	21
Spall	Scraper	6	56	140	14

Table 3: Significant results from secondary-level multivariate local Moran’s I analysis

Core Variable	Spatially Lagged Variable	#Of Clusters with significant Relationship
		High-High	Low-Low	Low-High	High-Low
Battered Biface	Flake Tool	2	77	45	1
Battered Biface	Hammer Stone	1	120	36	4
Battered Biface	Scraper	2	51	25	1
Biface	Flake Tool	2	69	42	9
Biface Preform	Scraper	1	53	25	2
Macroblade	Microblade	6	103	111	15
Microblade	Microblade core	7	66	116	15
Core	Flake Tool	2	68	43	13
Flake Tool	Scraper	7	44	19	19
Point	Scraper	2	47	25	12
Alberta Point	Macroblade	1	119	60	0
Cody Point	Macroblade	1	119	64	4
Impact Fractured Point	Flake Tool	1	77	43	3
Impact Fractured Point	Point	2	230	112	7
Impact Fractured Point	Scraper	0	49	28	3
Scraper	Point	39	185	77	51
Scraper	Impact Fractured Point	0	49	28	3
Scraper	Flake Tool	12	52	32	26
Spall	Flake Tool	3	73	41	5
Spall	Scraper	1	54	26	3

Maps of selected variable pair results display some interesting trends (Figures 4-7). For example, Figure 4a shows the association between Flake Tool and Scraper object types for primary-level clusters. While there are many High-High associations (as seen in Table 2), most of these are grouped in two locations at the north end of the study area. However, when the secondary-level cluster map for this association is compared (Figure 4b), these groupings have disappeared. Instead, new locations of High-High associations appear at this different scale. For the association between Point and Scraper (Figure 5), a similar pattern shows, with most of the High-High associations for primary-level clusters (Figure 5a) grouped in two locations at the north end of the study area. Note that the southern of these two High-High groups for Point and Scraper is in the same location as one of the Flake Tool to Scraper primary-level cluster groups. Again, these significant associations disappear at the secondary-cluster level (Figure 5b). At the first cluster level, Battered Bifaces and Hammerstones do not tend to occur together (Figure 6a), except for a single High-High cluster. At the secondary-cluster level, this High-High association has disappeared, and a new High-High association location has appeared, towards the northern portion of the study area (Figure 6b). It is interesting to note that this also occurs in the same location as one of the High-High groupings seen in both Figures 4a and 5a. Elsewhere in the reservoir, the general non-association trend between Battered Bifaces and Hammerstones holds at the secondary-cluster level. Other trends of interest include the globally significant positive correlation between Alberta Points and Macroblades. When the local associations are viewed on the map (Figure 7a), all of the High-High associations are grouped in one area, towards the center of the study area. The primary-level global negative correlation between Impact Fractured Points and Flake Tools is also visible in the local association types, as there are no High-High associations (Figure 7b). At the secondary-cluster level, the global association between Scraper and Point object types is apparent as several groups of High-High associations (Figure 7c). However, there are also several significant High-Low locations, most notably the very large group of these two association types which occurs in the northern part of the study area.

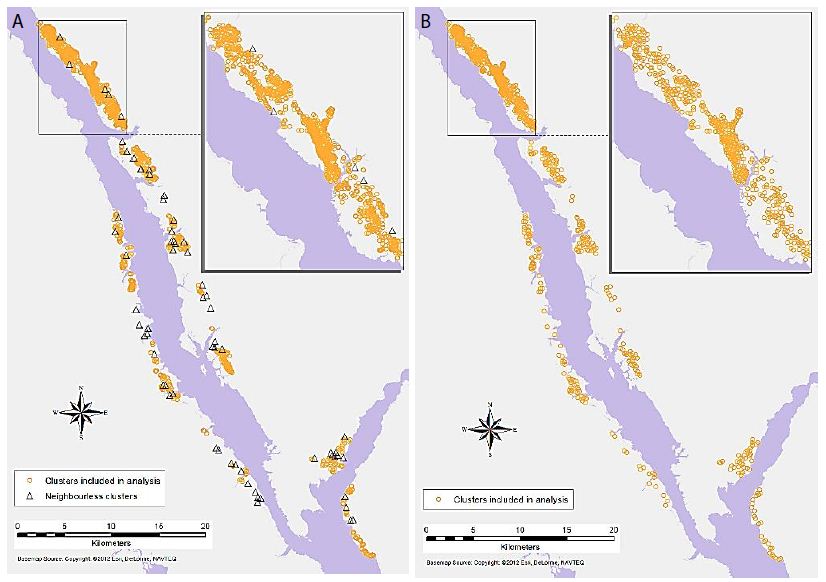
Figure 4: Significant associations between Flake Tool and Scraper object types for (a) primary-level clusters, and (b) secondary-level clusters (insignificant associations and neighbourless clusters omitted).

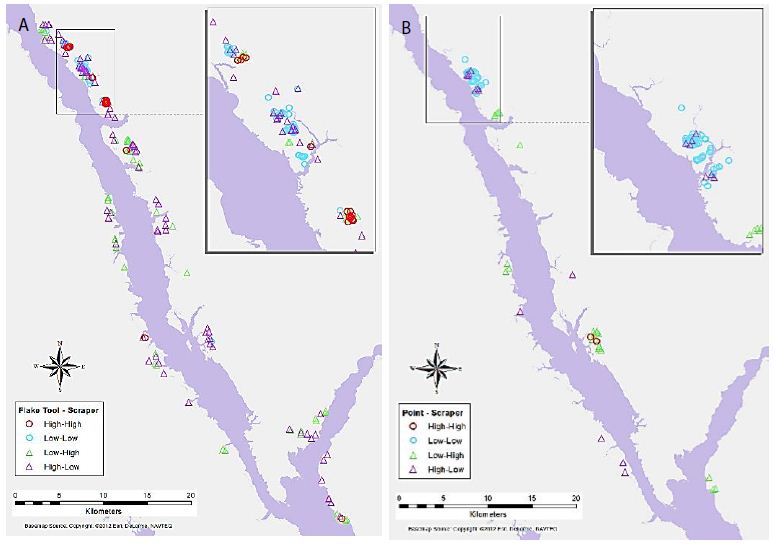
Figure 5: Significant associations between Point and Scraper object types for (a) primary-level clusters, and (b) secondary-level clusters.

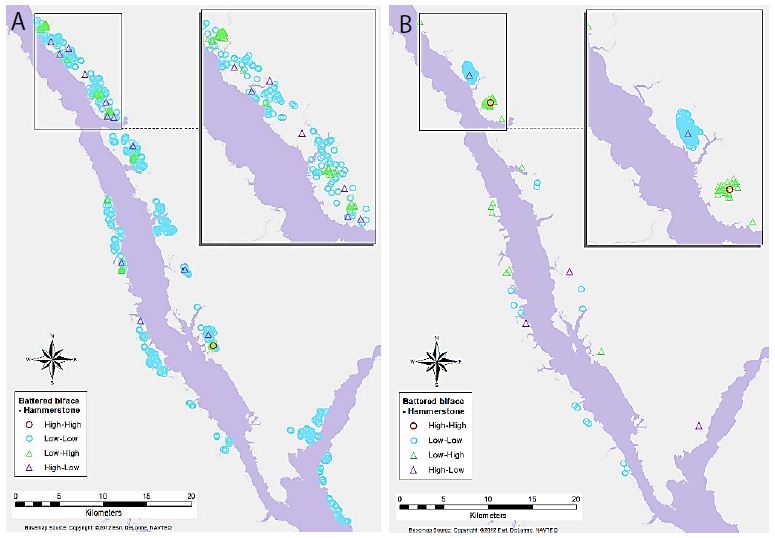
Figure 6: Significant associations between Battered Biface and Hammerstone object types for (a) primary-level clusters, and (b) secondary-level clusters.

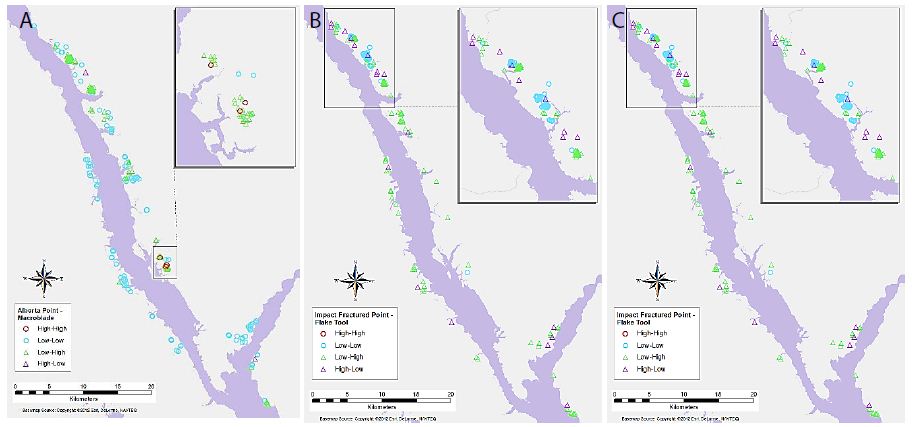
Figure 7: Significant associations between (a) Alberta Point and Macroblade object types for primary-level clusters, (b) Impact Fractured Point and Flake Tool object types for primary-level clusters, and (c) Scraper and Point object types for secondary-level clusters.

Discussion

Key results of the LISA analysis include the four global significant associations, between Alberta Points and Macroblades, Impact Fractured Points and Flake Tools as well as Scrapers, and Scrapers to Points. A number of interesting local patterns were also discovered, including the suggested High-High groupings seen at the same location for multiple object-pairs (Figures 4-6), and scale differences in these local patterns as highlighted by the use of two different levels of clustering. The significant relationships may have a number of explanations. The negative correlations between Impact Fractured Points and Scrapers/Flake Tools suggest that the Impact Fractured Points are hunting losses, rather than retrieved from a kill and then discarded at a campsite or butchering site. If the latter were the case, they would be expected to be found more frequently in association with Flake Tools and Scrapers, both of which object types would typically be found at camp or butchering locations. Furthermore, the Impact Fractured Point to Scraper results for secondary-level clusters. None of the clusters have a significant local High-High relationship at this level and, while not globally significant, this seems to follow the trend of the primary-level cluster results, thus implying that this relationship may persist at this scale across the site. The global relationship between Scrapers and Points at the secondary-cluster level was composed of several distinct groupings of local High-High associations. These may suggest significant use areas, such as regularly used butchering sites or campsites. However, perhaps of equal or greater interest is the area with a large grouping of High-Low significant associations, which oppose the global trend of positive correlation, suggesting that something quite different may be occurring in this particular region. The Alberta Point to Macroblade global association could indicate that these items were used contemporaneously, thus providing a possible scenario of temporal patterning. Though this association is not significant at the secondary-cluster level, even at this scale there are no clusters with high numbers of Alberta Points and low numbers of Macroblades and one second level cluster retains a significant local High-High association, suggesting that Alberta Points are not typically found far from Macroblades. Other local relationships observed have indicated some interesting trends that may have a number of explanations. The groups of High-High clusters seen in the same locations for several of the variable pairs (Figures 4-7) suggest that these are not likely to be randomly strewn artefacts but may be an indicator of some important activity areas, such as camp locations, though further research would be required to confirm this hypothesis. Hierarchical clustering has proven to be an effective tool for comparing the change in clusters over time, as well as the discovery of associations between different artefact types across multiple scales. The object type analysis revealed significant patterns in the association between different artefact types at multiple scales, and while it is not possible to draw a definitive conclusion of exactly what these relationships mean in terms of landscape use, they suggest a number of interesting hypotheses of possible uses and provide direction for further studies.

References

1. Carr C (1984) The Nature of Organization of Intrasite Archaeological Records and Spatial Analytic Approaches to Their Investigation. Advances in Archaeological Method and Theory 7: 103-222.
2. Bevan A, Conolly J (2009). Modelling spatial heterogeneity and nonstationarity in artefact-rich landscapes. Journal of Archaeological Science 36: 956-964.
3. Gillings M, Hacıgüzeller P, Lock G (2020). Archaeological Spatial Analysis: A Methodological Guide, Routeledge.
4. Anselin L (1995) Local Indicators of Spatial Association—LISA. Geographical Analysis 27: 93-115.
5. Okabe A, Funamoto S (2000) An exploratory method for detecting multi-level clumps in the distribution of points – a computational too, VCM (variable clumping method). Jouranl of Geographical Systems 2: 111-120.
6. Shiode S, Shiode N (2009) Detection of multi-scale cluster in network space. International Journal of Geographic Information Science 23: 75-92.
7. Kintigh KW, Ammerman AJ (1982) Heuristic approaches to spatial analysis in archaeology. American Antiquity 47: 31-63.
8. Voorrips A, O’Shea JM (1987) Conditional spatial patterning: Beyond the nearest neighbour. American Antiquity, 52: 500-521.
9. Clark PJ, Evans FC (1954) Distance to nearest neighbor as a measure of spatial relationships in populations. Ecology 35: 445-453.
10. Whallon R (1972) A new approach to pottery typology. American Antiquity 37: 13-33.
11. Moyes H (2002) The use of GIS in the spatial analysis of an archaeological cave site. Journal of Cave and Karst Studies 64: 9-16.
12. Kintigh KW (1990) Intrasite spatial analysis: A commentary on major methods. In Mathematics and Information Science in Archaeology: A Flexible Framework, edited by Albertus Voorrips. Studies in Modern Archaeology 3: 165-200.
13. Holdaway S, Witter D, Fanning P, Musgrave R, Cochrane G, et al. (1998). New approaches to open site spatial archaeology in Sturt National Park, New South Wales, Australia. Archaeology in Oceania 33: 1-19.
14. Hietala HJ, Stevens DE (1977) Spatial Analysis: Multiple Procedures in Pattern Recognition Studies. American Antiquity 42: 539-559.
15. Openshaw S (1984) The Modifiable Areal Unit Problem. Concepts and Techniques in Modern Geography, No.38, Norwick: Geo Books.
16. Buzzelli M (2020) Modifiable areal unit problem. In Kobayashi, A. (ed). International Encyclopedia of Human Geography, 2^nd, Elsevier, pg: 169-173.
17. Berry KJ, Kvamme KL, Mielke PW Jr. (1980) A Permutation Technique for the Spatial Analysis of the Distribution of Artefacts into Classes. American Antiquity, 45(1), 55-59.
18. Premo LS (2004) Local spatial autocorrelation statistics quantify multi-scale patterns in distributional data: an example from the Maya Lowlands. Journal of Archaeological Science 31: 855-866.
19. Murray AT, Estivill-Castro V (1998) Cluster discovery techniques for exploratory spatial data analysis. International Journal of Geographical Information Science 12: 431-443.
20. Wheeler DC (2007) A comparison of spatial clustering and cluster detection techniques for childhood leukemia incidence in Ohio, 1996-2003. International Journal of Health Geographics 6. [crossref]
21. Levine N (2004) CrimeStat III: A Spatial Statistics Program for the Analysis of Crime Incident Locations (Version 3.3): Ned Levine & Associates, Houston, TX, and the National Institute of Justice, Washington, DC.
22. Openshaw S, Charlton M, Wymer C, Craft A (1987) A Mark 1 Geographical Analysis Machine for the automated analysis of point data sets. International Journal of Geographical Information Systems 1: 335-358.
23. Estivill-Castro V, Lee I (2000a) AMOEBA: Hierarchical clustering based on spatial proximity using Delaunay diagram. Paper presented at the 9th International Symposium on Spatial Data Handling, Beijing, China.
24. Qu Y, Lee K, Lee I (2011) Cluster polygonization and qualitative cluster reasoning overview. Interntational Journal of Advancements in Computing Technology 3.
25. Yang X, He L, Lu H (2009) A New Method for Non-spherical and Multi-density Clustering. Third International Symposium on Intelligent Information Technology Application, 2009, pg: 35-38.
26. Estivill-Castro V, Lee I (2000b) AUTOCLUST: Automatic Clustering via Boundary Extraction for Mining Massive Point-Data Sets. Paper presented at the 5th International Conference on Geocomputation, University of Greenwich, United Kingdom.
27. Malik M, Singh P, Sharma DAK (2011) A novel spatial clustering approach for outlier detection & cluster generation by probing various distance matrices & Delaunay triangulation. International Journal of Computer Science and Technology 2: 104-108.
28. BC Hydro (2012) Williston Reservoir Retrieved August 24, 2012.
29. Eldridge M, Brunsden J, Parker A, Eldridge R (2008) Permit 2008-0179 BC Hydro 2008 Williston Dust Abatement Project Archaeological Impact Assessment Final Report: Millennia Research Limited.
30. Eldridge M, Thiesson V, Parker A, Eldridge R (2010) BC Hydro 2010 Williston Dust Abatement Project Archaeological Impact Assessment Final Report: Millennia Research Limited.
31. The Province of British Columbia (2022) Ministry of Forests, Lands, and Natural Resource Operations: Archaeology.
32. Glassow MA (1977) Issues in evaluating the significance of archaeological resources. American Antiquity, 42: 413-420.
33. Jenks GF (1967) The data model concept in statistical mapping. International Yearbook of Cartography 7: 186-190.
34. Anselin L, Syabri I, Smirnov O (2002) Visualizing Multivariate Spatial Correlation with Dynamically Linked Windows. New Tools for Spatial Data Analysis: Proceedings of the Specialist Meeting.
35. Anselin L (2022) GeoDa (Version 1.20): GeoDa Center for Geospatial Analysis and Computation.
36. Anselin L, Syabri I, Kho Y (2006) GeoDa: An Introduction to Spatial Data Analysis. Geographical Analysis 38: 5-22.