DOI: 10.31038/NAMS.2024711

Abstract

The paper develops a modelling for fluid and heat flows also in connection with diffusion processes in nanodevices. The approach involves rate equations that generalize those of Maxwell fluid and Maxwell-Cattaneo heat flux and is based on two basic principles of continuum physics: objectivity and thermodynamic consistency. From the technical side, the paper follows the view that a convenient procedure should be grounded on the theory of mixtures. Accordingly, within the classical theory of mixtures, the constitutive equations are established for stress tensor and heat flux in fluid-solid mixtures with relaxation properties. The results are then combined with models occurring in the literature about flow in porous media.

Keywords

Relaxation in nanosystems, Rate-type models, Porous media, Mixtures, Thermodynamic consistency, Objective derivative

Introduction

Among the features of nanodevices is the inefficient dissipation of heat, which can lead to material degradation. Consistently, the decrease of the thermal conductivity (see, e.g., [1-3]), which hinders heat exchange, calls for more involved materials models. Nanoscale systems with dimensions comparable to the mean-free path of particles (or phonons) nonlocal effects are required to be inserted in the model. Furthermore, in microdevices working at high frequencies also relaxation effects occur so that realistic models need to account for the time delay of relaxation processes. Diffusion processes are also of interest in nanodevices and this indicates that a proper modelling of fluid flow in porous media is required.

In essence, nonlocality and relaxation are modelled by means of spatial and time derivatives of suitable order in the equation of motion and the balance of energy. This paper develops a modelling for fluid and heat flows through an approach that is based on two principles: objectivity and thermodynamic consistency. Objectivity means that constitutive equations are form-invariant under the group of Euclidean transformations [4,5]. Thermodynamic consistency means that, granted the validity of the balance equations, the constitutive equations make the entropy production non-negative. For definiteness, from the technical side, this paper follows the view that a convenient approach should be grounded on the theory of mixtures. That is why we begin with the main points of the theory of mixtures. Next the constitutive equations are established for stress tensor and heat flux in fluid-solid mixtures with relaxation properties. The results are combined with models occurring in the literature about flow in porous media.

Notation and Balance Equations for Mixtures

The body under consideration is a mixture of n constituents occupying a time-dependent region of the three-dimensional space. The subscript α= 1, 2,…, n labels the fields pertaining to the α-th constituent and Σ_α is a shorthand for Σⁿ_α=1The compact notation is used; for any pair of vectors u, v the symbol u·v denotes the inner product,  and likewise for tensors,   The symbol ∇ denotes the gradient, ∇· the divergence, and ⊗ the dyadic product.

Denote by the subscript α= 1, 2, …, n the quantities pertaining to the α-th constituent. For any  function  the dashed symbol  denotes the material derivative relative to the pertinent constituent, viz.

The conservation of mass of single constituents results into the n continuity equations

The equations of motion are written in the form

where T_α is the (Cauchy) stress tensor, b_α the body force, m_α the interaction force, or growth, between constituents. The growths are subject to

No body couples are considered and then the balance of angular momentum results in

Let  be the specific internal energy. The local version of the balance of energy eventually reads

where  is the energy supply and

Lastly we look at the second law of thermodynamics which, also for mixtures, places restrictions on the admissible constitutive equations. For any α-th constituent let  be the absolute temperature and   the specific entropy. The balance of entropy is derived by the general view that the entropy change equals the entropy transfer plus the entropy production. This is made formal by letting j_α be the entropy flux,  the entropy supply and  the entropy production so that

The set of functions

constitutes a thermodynamic process. The axiom, known as entropy principle or second law of thermodynamics, about the increase of entropy in a closed system is stated by saying 2 that the entropy production is non-negative for any thermodynamic process consistent with the balance equations. Formally, for mixtures the second law of thermodynamics requires that

for any thermodynamic process.

This statement is based on refs [6-8]. Following [9] and [5], §9.3, we let the entropy productions   be given by constitutive equations, as is done for the entropy fluxes {j_α} after [7].

If the constitutive equations make the inequality non-valid then those constitutive equations are not admissible. That is why we can see the second law as the selection of physically admissible constitutive models.

For technical convenience we put

k_α being referred to as extra-entropy flux. Hence we can write eq. (4) as

Substitution of  from (3) results in

Using the Helmholtz free energy  we have

Hence the second law is expressed by the Clausius-Duhem (CD) inequality

We now investigate the thermodynamic requirements on the pertinent constitutive equations.

Solid-fluid mixtures

With the view of modelling porous media, we consider a binary mixture with a solid and a fluid; we denote by the subscripts f, s the quantities pertaining to the fluid and solid constituents. The fluid is viscous and compressible. To describe relaxation effects, both stress and heat flux are modelled through rate equations as is the case for the Maxwell (or Maxwell-Wiechert) fluid and the Maxwell-Cattaneo equation of the heat flux; account of nonlocality through higher-order derivative is developed in [10] via the Guyer-Krumhansl form.

Owing to objectivity, the rate has to be expressed through an objective time derivative. The simplest one is the corotational derivative namely

for vectors a and tensors A while W is the pertinent spin tensor (W_f or W_s). Hence we assume

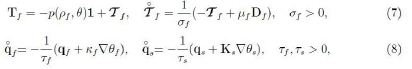
where K_s ∈ Sym is non-singular. If the rates vanish then eqs (7) and (8) reduce to the Navier-Stokes and Fourier laws; for formal simplicity the longitudinal viscosity coefficient is taken to be zero.

To frame these assumptions in a consistent thermodynamic setting we let

and derive the constitutive equations for  of the fluid and the solid. We let θ_f = θ_s = θ while ∇ θ_f ≠ ∇ θ_s. Then we observe that

we put m_f = − β(|u|)u, u = u_f − u_s, and hence

With these assumptions the extra-entropy fluxes k_f, k_s turn out to be zero; to save writing we omit them. Hence the CD inequality takes the form

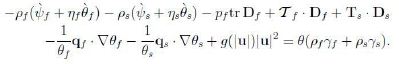
Compute  and observe that the relations

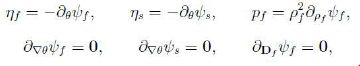
follow as a consequence of the linearity and arbitrariness of θ`<sub>f</sub>, θ`_s trD_f, (∇θ_f)`, (∇θ<sub>s</sub>)`, `D<sub>f</sub> . Next we recall the identity `E_s = F^T_sD_sF_s and notice that, by (7) and (8),

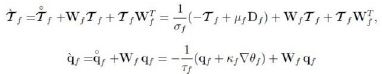
and the like for q_s. Thus we can write the remaining terms of the CD inequality as

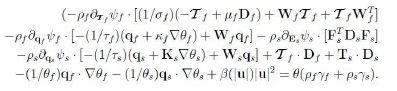
We first consider the dependence on W_f and W_s,

The linearity on W_f,W_s and the arbitrariness of  q_f, q_s imply that each term has to vanish; the vanishing of the second and third terms results in

Next since W ∈ Skw then for any tensors A,B we have 

hence   implies that

The linearity and arbitrariness of D_f,D_s, Δθ_f, Δθ_s imply

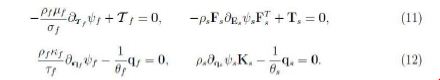
The CD inequality then reduces to

and hence each term has to be non-negative.

By using (11) and (12) we find

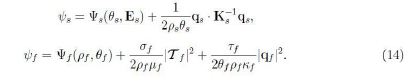
The symmetry conditions (9) and (10) hold identically while (13) holds if and only if

namely the expected relations for heat conductivities K_s, , shear viscosity μ_f, and interaction force coefficient β.

Dynamics of Viscous Fluids in Porous Media

The dynamics of the fluid is governed by the balance equations. With reference to the literature (e.g. [11] and refs therein), to simplify the notation we restrict attention to the fluid, omit the subscript f and use a superposed dot, ε˙, instead of a slash, ε’. The continuity equation and the equation of motion read

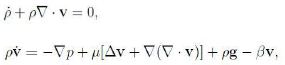
where g is the acceleration gravity. The function βv generalizes Darcy’s model through the Forchheimer function β while, as usual, it is assumed v_s = 0. According to (15) we have found that any β ≥ 0 is consistent with thermodynamics.

Things are more involved with the balance of energy, namely

By definition,

Hence the balance of energy involves  which requires that the rate equations (7), (8) are applied.

Conclusions

The thermodynamic analysis provides a complete scheme of dynamic equations for the flow of fluids in solids. Yet the general scheme so obtained is quite cumbersome thus justifying some approximations applied in the literature. Quite often β is taken to be constant but, foremost, the fluid is taken to incompressible, ∇ · v = 0, while 

The dependence of ε on  and q is not considered and (see, e.g., [12]) ε is assumed to depend only on the temperature θ.

According to eqs (14) and (16) the free energy ε is independent of  and q if

c₁, c₂ being positive parameters possibly dependent on  . Though this looks a very specific model, eq. (17) is the necessary assumption that makes ε (θ, ρ ) thermodynamically consistent if T_f and q_f are subject to the rate equations (7) and (8).

Acknowledgments

The research leading to this work has been developed under the auspices of INDAM-GNFM.

References

1. Hennessy MG, Myers TG (2020) Guyer-Krumhansl heat conduction in thermoreflectance experiments, in Multidisciplinary Mathematical Modelling. Applications of Mathematics to the Real World, F. Font and T.G. Myers eds, pp. 21-34, Springer Cham.
2. Cahill DG et al (2014) Nanoscale thermal transport, II Appl Phys Rev 1: 011305.
3. Dong Y (2015) Dynamical Analysis of Non-Fourier Heat Conduction and Its Application in Nanosystems, Springer, New York.
4. Truesdell C (1984) Rational Thermodynamics, Springer, New York.
5. Morro A, Giorgi C (2023) Mathematical Modelling of Continuum Physics, Birkh¨auser, Cham.
6. Truesdell C (1969) Rational Thermodynamics: A Course Of Lectures On Selected Topics, McGraw-Hill, New York.
7. M¨uller I (1968) A thermodynamic theory of mixtures of fluids. Arch Rational Mech Anal 28: 1-39.
8. Bowen RM (1968) Thermochemistry of reacting materials. J Chem Phys 49: 1625-1637.
9. Morro A (2022) Diffusion models of continuum physics. Nanotechnol Adv Mater Sci. 5: 1-6.
10. Morro A (2023) On the Modelling of Heat Conduction in Crystals via Higher-grade Terms. Nanotechnol Adv Mater Sci 6 (3): 1-4.
11. [11] Straughan B (2023) Thermal convection in a Brinkman-Darcy-Kelvin-Voigt fluid with a generalized Maxwell-Cattaneo law. Ann Univ Ferrara 69: 521-540.
12. Payne LE, Song JC (1997) Continuous dependence on initial-time geometry and spatial geometry in generalized heat conduction. J Math Anal Appl 214: 173-190.