DOI: 10.31038/NAMS.2022514

Abstract

The interaction between two metallic spheres with radius R with external electromagnetic (EM) field polarized in the symmetric  direction is described Solutions of Laplace equation with bi-spherical coordinates are developed Hot spots are obtained under the condition that the shortest distance between the two spheres surfaces is very small relative to their radius. Boundary conditions are applied which assume very large real negative value for the dielectric constant of the metallic spheres. Under these conditions the EM field is amplified by many orders of magnitudes relative to the incident EM field. Analytical results for maximal Raman enhancement factor (EF) are obtained as function of various parameters. The present study can be applied to surface-enhanced Raman spectroscopy (SERS) and two-photon induced illumination (TPI-PL) in which the amplification is proportional to the fourth power of the incident EM field.

Introduction

An electromagnetic (EM) mechanism for surface enhanced Raman spectroscopy (SERS) involves the localization and amplification of incident light fields by a surface plasmon resonance. Motivated by the need to quantify the EM enhancement within such structures, computational studies using the finite element method (FEM), the finite-difference time domain (FDTD) method, discrete dipole approximation, and the generalized multipole Mie (GMM) analysis appeared as ideal complement to experimental studies [1,2]. The ability of SERS to obtain single-molecule sensitivity relies on the formation of regions with ultra-highly enhancement called hot spots. These highly enhancement sites occur at the junction between two and more plasmonic structures separated by a very small gap. In the limit of very small particles, the EM interaction between different parts of the metal is instantaneous. Then Maxwell equations are leading to the condition that the electric and magnetic fields are longitudinal (). The magnetic response of the particles is negligible at optical frequencies for very small particles so that the electric field is the gradient of the scalar electric potential,    [3]. In the present work analytical results are developed for maximal SERS enhancement factor ( EF ) under such conditions for two nearby metallic spheres. It is of much importance to find the conditions under which the EF is maximal so that spectroscopic effects on one molecule level can be observed. Although we treat a very special system one can learn from this case about the general conditions for getting maximal EF.

We consider two metallic spheres of equal radius R described in Figure 1. We choose the vertical z-axis along the line passing through the centers of the spheres. The perpendicular x, y  plane contains the midpoint between the two spheres. We assume that the distance from the center of one sphere with radius, R (the upper one) to the center of the coordinate system along the Z  coordinate is +D and that for the other sphere with the same radius R (the lower one) is -D.

We define

                    (1)

The shortest distance between the two spheres surfaces is given by: 2δ. For simplicity we treat mainly the case where the incoming EM field is homogenous and the electric field 2δ is along the Z axis. Assuming certain values for the dielectric constants [4,5] (for the two spheres ε(ω) which are function of the frequency ω and for the surrounding medium ε1) we present the solutions of the Laplace equation for the limiting case for which δ<1. The two focuses F₁and F₂  are located at a distance α from the center of the coordinate system along the symmetric  axis, in upper and lower directions, respectively.

Laplace equations solutions for the upper and lower spheres are given by Ψ₊ and Ψ_– , respectively, and Laplace equation solution for the surrounding medium is given by Ψ1. The present system has a cylindrical symmetry under rotation around the Z axis. Thus, the two focuses are not changed by this rotation. It was shown [6-9] that Raman signals are strongly amplified when the molecules are inserted in the interstitial gaps between nanoparticles due to the very strong EM fields induced in these gaps (“hot spots”). Special studies were made on Raman signals enhancement in dimers (two nanoparticles) [10,11]. It was found that the Raman signals of spherical dimers are strongly enhanced when the incident polarization is parallel to the inter particle axis of the dimer (parallel polarization) [12]. In this case the opposite charges of polarization are facing each other at the small gap and by their interaction generate a huge EM field. On the other hand, when the incident EM field is polarized in direction perpendicular to the inter particle axis (perpendicular polarization) the induced charges are in directions different from that of the gap. In this case, individual local surface plasmons (LSP) in the dimer do not interact strongly with each other. As a result, EM field interaction is approximately compared in this case with that of isolated particles. It was found that the signal in SERS is proportional to the fourth power of the amplified EM field for parallel polarization. Similar results are obtained by two-photons-induced luminescence (TPI-PL) [13]. Raman scattering and TPI-PL phenomena are increased by many orders of magnitude relative to that of the ordinary ones, for molecules inserted in these hot spots.

In the present work we study the solutions of Laplace equation solutions for dimers with bi-spherical coordinates [14,15] which are developed under the condition 2δ<1. Hot spots are produced in the system of two metallic spheres interacting with external homogeneous EM field. While important results (mainly for the potential) for the present system were developed by solving Laplace equation with the use of bi-spherical coordinates the analysis for the hot spots remained problematic due to convergence problems. By using boundary conditions various authors [16] obtained after some tedious algebra set of recursion relations (or equivalently infinite set of linear equations) for the Laplace equation superposition solutions. Such system was truncated by taking finite set of linear equations and was solved on computers. Special care was taken to make sure its convergence i e , that the number of recursion relations is not too small (especially for nearby spheres where very high number of recursion relations is needed). We give here an alternative for deriving the EM fields at the hot spots by using bi-spherical coordinates with certain approximations. We develop in the present work a relatively simpler model for analyzing the properties of the EM fields by using approximations which are suitable for treating the hot spots with the use of bi-spherical coordinates. Analytical results for maximal enhancement factor (EF) are developed. The bi-spherical coordinates are a special three-dimensional orthogonal coordinates system defined by coordinates η, α, Φ.

The two poles with η = ±∞ are located on the Z axis at z = ±a and denoted in Figure 1 by F₁ and F₂. Surfaces of constant η are given by spheres (described in Figure 2).

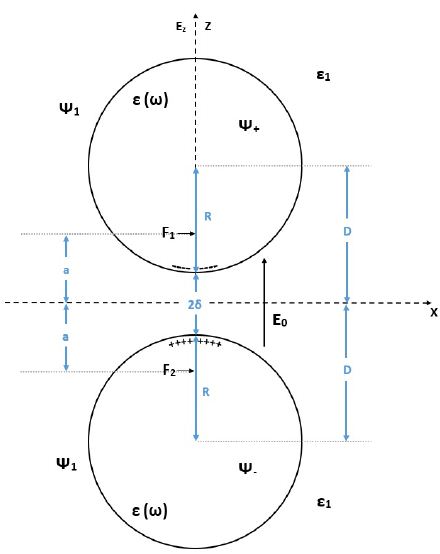
Figure 1: Two spheres with metallic dielectric constant ε(ω) with radius R and the surrounding medium with dielectric constant ε₁, under homogenous external EM field propagating in the x direction and polarized in the Z direction where E_z = E₀. Various parameters are described in the present x, z coordinates system.

In the present system the electrostatic potential has cylindrical symmetry about the Z axis. It is therefore independent of the angle Φ and only the term m=0  is retained. In Figure 2 we describe the coordinates η for certain values of η as function of the x, z  coordinates. The large circles represented by small values of η are truncated in this figure. The surfaces of the spheres in the present system are given by bi-spherical coordinates ±η₀  given by:

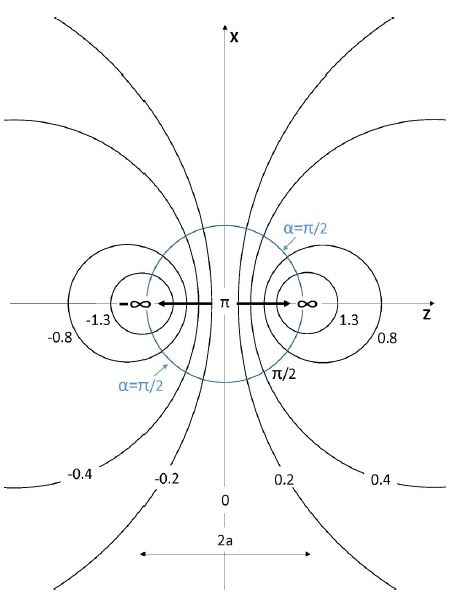
Figure 2: Bi-spherical coordinates in the x, z plane showing circles of constant bi-spherical radial coordinate η where curves of constant polar angular α with α =π ,π / 2,π / 3,π / 6 are perpendicular to these curves [3]. EM field polarized in the Z direction propagates in the x direction. The curve for α =π is along the Z axis.

This equation for η = η₀ ( η = – η₀ ) represents in Figure 1 the upper (lower) sphere with radius R  where its center is moved from the center of the coordinate system by a distance D in the positive (negative) Z direction. In Figure 2 η₀ should be chosen for a special value of η which is related by Eq (3) to the parameters of Eq (1). The distance between the surfaces of the two spheres along the Z axis becomes very small relative to their radius for small values of η ( η = η₀ < 1). The two poles F₁ and F₂ are obtained at Ψ₊ , Ψ_– .

Laplace-Equation Solutions for Two Metallic Spheres with Incident EM Field Parallel to the Symmetric Z Coordinate

We define Ψ₊ , Ψ_–  and Ψ₁, respectively, as the potentials (with the condition m=0 ) inside the upper sphere, the lower sphere, and the surrounding medium, respectively. The potential due to the external field   is assumed to be given by  . In the present article the external field is written in short notation as E₀. It is antisymmetric with respect to reflections through the xy plane: Z → – Z or η → – η.

The potential  Ψ₁ outside the spheres is given with the same symmetry as that of the external field potential:

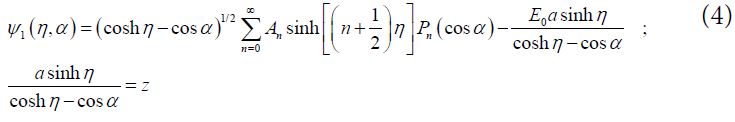
where P_n are Legendre polynomials and A_n  are certain constants. Using the relation [16-20]:

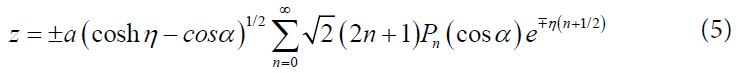
where the upper (lower) sign holds for positive (negative) Z, Eq (8) is transformed to:

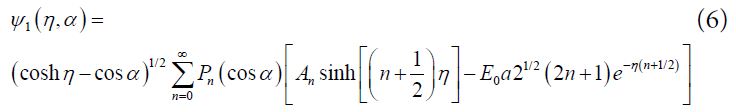
For η = η₀ , and positive Z, Eq (6) is transformed to:

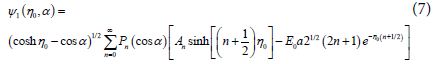
From the fact that  Ψ₊ and Ψ_– have to be finite at the points: x = y = 0; z = ±a, where: η = ±∞, we obtain [16-20].

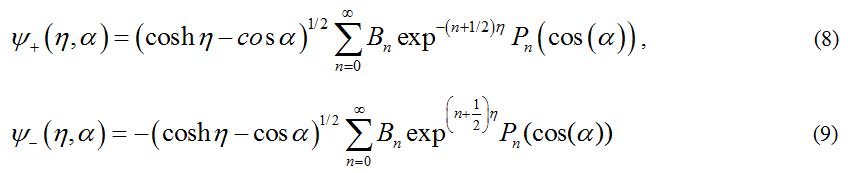
One should notice that the function 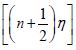  is antisymmetric with respect to reflections through the xy  plane i.e. Z → – Z or η → – η in agreement with the symmetry of the external electric field. The general solutions for the potentials in the surrounding medium, and in the upper sphere are given by Eqs (6) and (8), respectively. But the coefficients  A_n  and B_n  should be obtained from the boundary conditions.

Using Eqs (6-9) we get the EM potentials as function of the bi-spherical coordinates. Transformation of these equations to be functions of the  x, y, z coordinates can be made by using Eqs (2). The coefficients  A_n  and B_n are calculated as follows:

We use the first boundary condition given as:

By using the equality (10) and comparing the corresponding expressions (7) and (8) for η = η₀ we obtain:

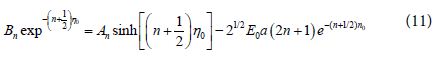
A second boundary condition can be used as [16-20]:

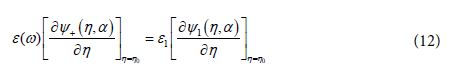
Using Eq (6) we get:

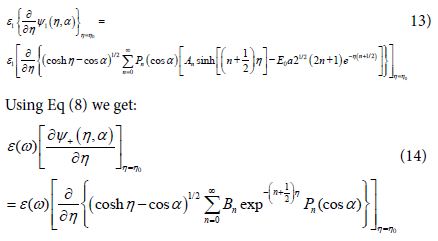
The derivatives 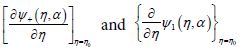  include the local plasmons charges induced on the surfaces of the spheres. In the present work we follow the idea, that for treating the limits of large field enhancement in hot spots we can use the following approximation which will simplify very much the analysis:

a) Derivatives in Eqs (13) and (14) include derivatives according to η of (cosh η – cos α )^½ in addition to the derivatives of the terms in the summations of these equations. Under the condition that δ is much smaller than R there are many B_n and A_n terms including exponential terms with derivatives proportional to the integer n which are very large relative to the derivatives of (cosh η – cos α )^½ so that the latter derivatives can be neglected for hot spots. The terms with larger value of n for 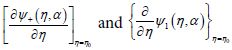 represent more rapid decay of the local surface plasmons.

b) In the present analysis for hot spots we assume that A_n and B_n are very large numbers so that for the purpose of using the boundary condition (12) the small term  can be neglected.

By substituting Eqs (13) and (14) into Eq (12) and using the above approximations we get for the relation between A_n and B_n:

Here the common factors: (cosh η – cos α )^½ ,  P_n ( cos α ) ,  and the term of order n proportional to E₀ were neglected Eq (15) shows that for larger values of −ε (ω) the term B_n becomes smaller. One should notice that while Eq (15) represents an approximate relation for hot spots, Eq (11) is exact one. One might notice that the above approximation b) was not included in [3]. We find now that although the derivative of  (cosh η – cos α )^½  is small relative to the derivatives of exponential terms its contribution might be not small relative to the term with external field. So only by using both approximations the new relation (15) between B_n and A_n is approximately valid at hot spots.

By substituting Eq (15) for B_n 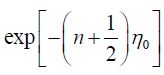 into Eq (11) we get:

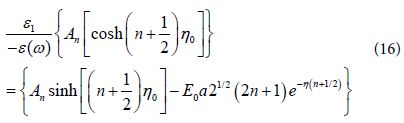
By rearranging the terms in Eq (16) we get:

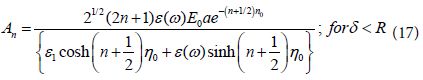
One might notice that the expression for A_n derived in [3] included the same denominator as in Eq (17) but the numerator becomes now different due to the use of the approximate relation of Eq (15). In the following analysis we develop new analytical results for EF which were not obtained in previous works as they ended there only with numerical calculations.

By transforming the hyperbolic functions of Eq (17) to exponential terms we get:

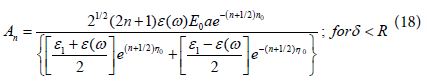
We divide both numerator and denominator of this equation by  . Then we get

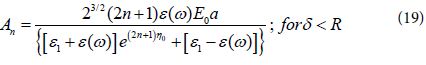
We note that the calculation of the coefficients A_n by the use of Eq (19) becomes quite simple as it can be derived in a straight forward way by the use of the parameter ε (ω ) and the experimental parameters: ε (ω), and ε₁. The use of the present approach is limited, however, by the validity of Eq, (15) appropriate to hot spots. For more accurate calculations we should add the contribution of the derivatives of (cosh η – cos α )^½ but this will complicate very much the analysis so that new results for EF were not obtained [17-20].

For getting maximal  EF one uses metals of the type of  Au or  Ag which at certain frequencies ε(ω)  is very large real negative value (taken as experimental parameter) with negligible imaginary value. In the following Section we will develop the equations with bi-spherical coordinates for the electric field at the hot spots. We will develop further our equations by bi-spherical coordinates in Section 4 for the limit of enhancement factor (EF) under the above conditions and approximations. The requirement of having large negative real value for the metals dielectric constant will be found to be a crucial parameter for large EF [21-30].

The EM Field in Bi-Spherical Coordinates at the Hot Spots

The normal component of the EM field   for which m=0 [16] is related in the space outside of the two spheres to the gradient in bi-spherical coordinates given as:

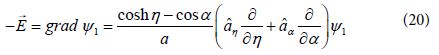
where ,  are unit vectors in the  directions, respectively, i e in the bi-spherical radial direction   and in direction perpendicular to  .

Since the potential Ψ₁ in bi-spherical coordinates is given in Eq (10) by sum of n terms, the gradient in the normal η direction is given by:

In the derivation for gradient of the potential for the normal component (in the radial direction) only derivatives relative to η are taken into account while η₀ and α remain certain constants. By operating with Eq, (21) on Ψ₁ ( η , α ) of Eq (10) we take into account only the derivatives of the terms proportional to A_n representing the amplified potential which is very large relative to the external potential terms -E₀ Z. Then we get:

Since the derivative of (cosh η – cos α )^½ relative to η is very small relative to the derivatives of the sinh functions (for δ <1 where the number of coefficients A_n is very large) we neglect this derivative and get

Eq (23) gives the general solution for the radial EM field in bi-spherical coordinates for hot spots for which δ <1 and for which the coefficient A_n are given by Eq (19).

Following Figure 2 and previous analysis we find that the hot spot is produced in a region for which the bi-spherical coordinate α satisfy approximately the relation α =π →c osα = −1. One should notice that the curve α = π coincides with the z axis, connecting the two poles with η = ±∞ and it is perpendicular to all η curves. It leads to special values of the Legendre polynomials on the symmetric  Z axis given by [3]:

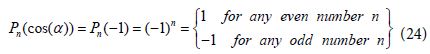
By substituting the value cos α = −1  and Eq (24) into Eq (23) we obtain the result for the EM field in bi-spherical coordinates on the symmetric coordinate  Z including the hot spot:

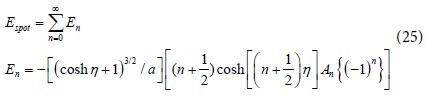
We are interested in calculations of the total EM field intensity at the hot spot given by E_spot² . We notice that in the calculation of E_spot² we have non-diagonal products E_nE_n , (n ≠ n^`’ ) with alternating signs so that their total contribution approximately vanishes. We consider therefore only the diagonal incoherent elements. Then for the electric field amplified factor E_spot² and for the SERS measurements which are proportional to E_spot⁴ we get:

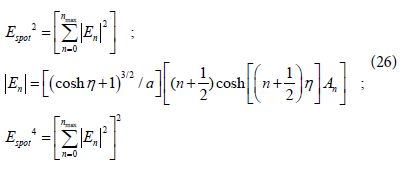
We should take into account that E_spot² gives the electric field squared at the hot spot where products of E_n with E_n , ( n ≠ n^`’ ) vanish due to the approximation made after Eq (24). We should consider also that SERS measurements depend on E_spot⁴ so it is obtained by the square of the sums of Eq (26) (as demonstrated later in Section 4). We inserted in Eqs (26) the maximal value n_max which guarantees summation convergence but in the analytical calculations we allow this value to tend to ∞. Transformations of the η coordinate to be a function of the Z coordinate were developed in previous work but here we develop the explicit results for EF at the center of the hot spot for which η = 0. Then Eq (26) is transformed to simpler form as:

The η coordinates for the hot spots are in the range 0 ≤ η ≤ η₀ so that we expect that for larger values of η we will get larger values of  corresponding to larger values of the  functions. While such effect might be important, for cases for which η₀ < 1 such effect will be relatively small so that Eq (27) still gives an approximate order of magnitude to Eq (26).

Analytical Results for Maximal Field-Enhancement (EF) at the Center of the Hot Spot

The electric field  at the center of the hot spot is obtained by inserting Eq (19) into Eq (27) with summation over η. Then we get:

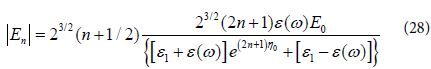
We define the light intensity as 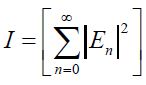 . Then the amplification of the light intensity at the center of the hot spots is given by:

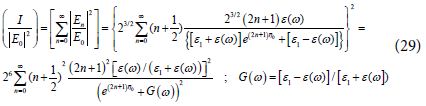
One might notice that the parameter G(ω) in the present analysis is based on the new equation (15)

Eq (29) can be converted approximately to the following integral:

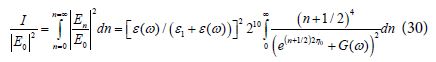
Eq (30) was transformed by using the definitions:

and given approximately as

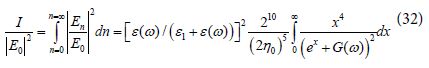
By assuming a very large real negative value of ε (ω) we get from Eq (29) the approximation G(ω) → −1, Then by using this approximation in Eq (32) we get:

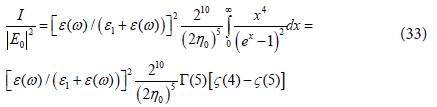
The integral in Eq (33) is obtained by using the corresponding integral from Gradshtein and Ryzhik book [31] where Γ(n) is the Gamma Function and ς (n) is the Riemann Zeta Function with the values.

Inserting these values in Eq (33) we get:

As the amplified field in SERS measurements is proportional to the fourth power its field enhancement factor (EF) is given by the square of Eq (35) i e ,

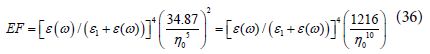
Eqs (35-36) represent very fundamental results by which the maximal enhanced light amplification factor for symmetric metallic dimers is proportional to η₀^-5 and the EF for SERS measurements is proportional to η₀^-10 . These analytical results are valid under the conditions 2δ <1, and G (ω) = [ε₁ −ε (ω)] / [ε₁ +ε (ω ) ] ) → −1  For cases in which G (ω) = | [ε₁ −ε (ω)] / [ε₁ +ε (ω ) ] )| >1 the integral in Eq. (32) is changed reducing much its value. It is verified by our calculations by which:

For example, for  G (ω) = [ε₁ −ε (ω)] / [ε₁ +ε (ω ) ] ) = −1.1, -1.2, -1.3 we get, respectively, F(ω) = 0.707,0.232,0.159  so that the integral in Eq (32) becomes smaller and the light intensity of Eq (35) is decreased by the function F(ω). The EF of Eq (36) is decreased by this function squared (The changes in the coefficient ε (ω) / ( ε₁ + ε (ω ) ) are relatively smaller). An important conclusion from the present analysis is that for getting maximal EF we need to use metals which have large real negative value for ε (ω) i.e. using metals like A_u or A_g at certain frequencies. For hot spots for which we have the condition 2δ <1 we can use the approximations:

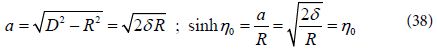
We find that the critical parameter η₀ for the symmetric spherical dimers is   where d = 2δ is the shortest distance between the two spheres. We estimate that in more general nano particles gaps the critical parameter will be the ratio between the length of the gap and the metallic curvature around it.

Conclusion

In the present work we treated the mechanism by which “hot spots” are produced in the system of two metallic spheres with the same radius R interacting with incident homogeneous EM field polarized in the symmetric  Z direction. Hot spots with huge EM field are produced by local plasmons at a small gap with nanoscale dimensions. Such hot spots are measured by surface enhanced Raman spectroscopy (SERS) and two-photon induced luminescence (TPI-PL). These effects depend on the fourth power of the EM field at the hot spot where the measured molecules are inserted. The present analysis is based on theoretical solution of Laplace equations using bi-spherical coordinates with certain values for the dielectric constants of noble metals. In the present system the fourth power of the EM fields at the hot spot turns to have extremely large values when the shortest distance between the spheres surfaces 2δ is very small i e , when 2δ <1. We developed in the present article certain approximations suitable for hot spots. In the present system in which the external EM is in the symmetric  Z axis the potential has cylindrical symmetry about the Z axis. Therefore the potential Ψ₁ (η,α)  at the hot spot developed in Eq (10) is function of the bi-spherical coordinates η, α , where  represents the distance from the bi-spherical coordinates center and η,α represents an angle from this reference direction. The coordinates η,α can therefore be described as bi-spherical polar coordinates in the x, z plane of Figure 1, and these coordinates are not changed by rotation around the z axis. The potential Ψ₁ (η,α) is proportional to summation of Legendre polynomials P_n (α)  with proportionality coefficients A_n and sinh function. The last term on the right side of Eq, (10) represents the external potential V_ext = – EZ where Z is defined in bi-spherical coordinates in Eq (2), and E₀ denotes, in short notation, the external EM field. By using the boundary conditions, we obtained after some calculations and certain approximations a general equation for the coefficients A_n in Eq (19). General solution for the EM field in the bi-spherical radial direction η is derived in Eq (23). Amplified EM field is found to be proportional to sum of products of the coefficients A_n with Legendre polynomial P_n (cos α) and with cosh function. As the hot spots in dimers are produced on (or near) the symmetric Z axis, for which x=y=0 we simplified the calculations by using this condition and used the relation: cos α = -1 simplifying the expression for Legendre polynomials. The use of bi-spherical coordinates is demonstrated in Figure 2. In Section 4 we developed analytical results for the field enhancement factor (EF) at the center of the hot spot. Although the electric field has a complicated dependence on the coordinate Z for simplicity of calculation we used Eq (27) for the hot spot center. The final results are given in Eq (35) in which the maximal light amplification factor is proportional to η₀^–5 and in Eq (36) in which the maximal EF for SERS measurements is proportional to η₀^-10 where  and  d = 2δ is the shortest distance between the two spheres. The present article is based on classical model but when the gap length is of an atomic scale quantum effects become important [32].

References

1. Kleinman SL, Frontiera RR, Henry A-I, Dieringer JA, Van Duyne RP (2013)Creating, characterizing, and controlling chemistry with SERS hot spots. Phys ChemChem Phys 15: 21-36. [crossref]
2. Sonntag MD, Klingsborn JS, Zrimsek AB, Sharma B, Ruvuna LK et al. (2014) Molecular plasmonics for nanoscale spectroscopy. Chem Soc Rev 43: 1230 [crossref]
3. Ben-Aryeh. (2021)Hot spots in two metallic spheres system related to Laplace equation solutions with bi- spherical coordinates. Applied Physics B 127: 157. [crossref]
4. Johnson PB, Christy R W (1972) Optical constants of the noble metals. Phys Rev B 6: 4370-4379.
5. Joh Johnson PB, Christy RW (1974) Optical constants of transition metals: Ti, V, Mn, Fe, Co, Ni, and Pd. Phys Rev B 9: 5056-5070.
6. Le Ru EC, Etchegoin PG (2009) Phenomenological local field enhancement factor distributions around electromagnetic hot spots. J Chem Phys 130: 181101. [crossref]
7. Ding SY, You E M, Tian ZQ, Moskovits M (2017) Electromagnetic theories of surface-enhanced Raman spectroscopy. Chem Soc Rev 46: 4042-4076. [crossref]
8. Inoue M, Ohtaka K (1983) Surface enhanced Raman scattering by metal spheres. I. cluster effect. J Phys Soc Japan 52: 3853-3864.
9. Jiang J, Bosnick K, Maillard M, Brus L (2003) Singe molecule Raman spectroscopy at the junctions of large Ag nanocrystals. J Phys Chem B 107: 9964-9972.
10. Nikoobakht B, El-Sayed MA (2003) Surface-enhanced Raman scattering studies on aggregated gold nanorods. J Phys Chem A 107: 3372-3378. [crossref]
11. Lee HM, Lee JH, Jin SM, Suh YD, Nam JM (2013) Single-molecule and single-particle-based correlation studies between localized surface plasmons of dimeric nanostructures with 1 nm gap and surface-enhanced Raman scattering. Nano Letters 13: 6113-6121. [crossref]
12. Li W, Camargo PHC, Lu X, Xia Y (2009) Dimers of silver nanospheres: Facile synthesis and their use as hot spots for surface-enhanced Raman scattering. Nano Lett 9: 485-490.
13. Imura K, Okamoto H, Hossain MK, Kitajima M (2006) Visualization of localized intense optical fields in single Gold nanoparticle assemblies and ultrasensitive Raman active sites. Nano Letters 6: 2173-2176. [crossref]
14. Aravind PK, Nitzan A, Metiu H (1981) The interaction between electromagnetic resonances and its role in spectroscopic studies of molecular adsorbed on colloidal particles or on metal surfaces. Surface Science 110: 189-204.
15. Morse PM, Feshbach H (1953) Methods of Theoretical Physics.
16. Stoy RD (1989) Solution procedure for the Laplace equation in bi-spherical coordinates for two spheres in a uniform external field: Parallel orientation. J Appl Phys 65: 2611-2615.
17. Stoy RD (1989) Solution procedure for the Laplace equation in bi-spherical coordinates for two spheres in a uniform external field: Perpendicular orientation. J ApplPhys 66: 5093-5095.
18. Ruppin R (1978) Surface modes of two spheres. Phys Rev B 26: 3440-3444.
19. Goyette A, Navon A (1978) Two dielectric spheres in an electric field. Phys Rev B 13: 4320-4327.
20. Levine HB, McQuarrie DA (1968) Dielectric Constants of simple gas. J ChemPhys 47, 4181-4187.
21. Yan BX, Zhu YY, Wei Y, Pei H (2021) Study on surface enhanced Ramanscattering of and sphericl dimers based on 3D finite element method. Scientific Reports 11: 8391. [crossref]
22. D DePrince AE, Hinde RJ (2010) Accurate computation of electric field enhancement factors for metallic nanoparticles using the discrete dipole approximation. Nanoscale Res Lett 5: 592-596. [crossref]
23. Drai Draine BT, Flatau PJ (1994) Discrete-dipole approximation for scattering calculations. J Opt Soc Am A 11: 1491-1499.
24. Camargo PHC, Au L, Rycenga M, Li W, Xia Y (2010) Measuring the SERS enhancement factors of dimers with different structures constructed from silver nano-cubes. Chem Phys Lett 484: 304- 308.
25. Le Ru EC, Blackie E, Meyer M, Etchegoin PG (2007) Surface enhanced Raman scattering enhancement factors: A comprehensive study. J Phys Chem C 111: 13794.
26. Stiles PL, Dieringer JA, Shah NC, Van Duyne RP (2008) Surface enhanced Raman spectroscopy. Annu Rev Anal Chem 1: 601-626.
27. Etchegoin PC, Le EC (2011) Basic electromagnetic theory. In Surface -Enhanced Raman -Spectroscopy. Wiley
28. Yu H, Peng Y, Yang Y, Li ZY (2019) Plasmon-enhanced light-matter interactions and application. Computational Materials 5: 45.
29. Jensen T, Kelly L, Lazarides A, Schatz GC (1999) Electrodynamics of noble nanoparticles and dimers. J Cluster Science 10: 295-317.
30. McMahon JM, Li S, Ausman LK, Schatz GC (2012) Modelling the Effects of small gaps in surface-enhanced Raman Spectroscopy. J Phys Chem C 116: 1627-1637. [crossref]
31. Gradshtein IS, Ryzhik IM (1980) Table of Integral, Series and Products New York, Academic Press p: 330.
32. Zhu W, Esteban R, Borisov AG, Baumberg JJ, Nordlander P, et al. (2016) Quantum mechanical effects in plasmonic structures with sub-nanometer gaps. Nature Communications 17: 11495. [crossref]