DOI: 10.31038/NAMS.2023613

Abstract

In this article, an interesting phenomenon has described the geometries and vibrational frequency of the stable Au_N clusters with N=56 and 57. We have found all 2 clusters are having the very same C₁ point symmetry group. For the re-optimization process, the finite-differentiation method has been implemented within the density-functional tight-binding (DFTB) approach. The effects of the range of interatomic forces were calculated and the desired set of system eigenfrequencies (3N-6) are obtained by diagonalization of the symmetric positive semidefinite Hessian matrix. More than anything else, we have observed the vibrational spectra, which occur between 1.57 cm⁻¹ and 336.04 cm⁻¹ at ∆E=0. Most significantly, all the clusters had come across the double and the triple-state degeneracies, which are due to the stretching and the bending mode of the vibrations through the atoms. Nevertheless, the vibrational spectrum is strongly dependent upon size, shape, and structure.

Keywords

Gold atomic clusters, Density-functional tight-binding (DFTB) approach, Finite-difference Method, Force constants (FCs) and vibrational spectrum

Introduction

Gold nanoclusters are promising optically functional materials because of their attractive optical properties, such as luminescence, two-photon absorption, photothermal conversion, and photodynamics. Regulating the optical functions of gold nanoclusters and improving their performance have attracted wide interest in biological applications. Noble metal like rhodium (Rh), palladium (Pd), silver (Ag), platinum (Pt), and gold (Au) is one kind of modish and desired material, according to their inherent resistance to oxidation and corrosion even in the moist environment. Its physical and chemical properties appear to be entirely change as the size of metal continuously decreases into nanoscale because of the quantum size effect, surface effect, small size effect, and macroscopic quantum tunnelling (MQT) effect [1-5]. Nanoclusters have potential uses in chemical reactors, telecommunications, microelectronics, optical data storage, catalysts magnetic storage, spintronic devices, electroluminescent displays, sensors, biological markers, switches, nano-electronics, nano-optics, transducers and many other fields. In general, Noble-metal (Cu, Ag, and Au) clusters have attracted much attention in scientific and technological fields because of their thermodynamic, electronic, optical and catalytic properties in nano-materials. Especially, gold is a soft metal and is usually alloyed to give it more strength as well as a good conductor of heat and electricity, and is unaffected by air and most reagents, those are the main reasons to choose among the other metal clusters [6-10].

In this study, mainly we focus on the vibrational properties of gold atomic clusters with sizes Au_51-54 atoms, because, the vibrational properties play a major role in structural stability [11-18]. For further assistance for the readers, specifically for the general information about global minima gold structures which have been calculated by the work of Dong and Springborg [19,20] can be found in those articles. In very short, the structures were found through a so-called genetic algorithm (GA) in combination with Density Functional Tight-Binding (DFTB) energy calculations and the steepest descent algorithm permitting a local total energy minimization. Nevertheless, in our case, we use the numerical finite-difference method [21] along with the density-functional tight-binding (DFTB) approach and finally extract the vibrational spectrum from the optimized structures. Overall, for a better understanding and to visualize, the detailed information is discussed in the results and discussion section.

Theoretical and Computational Procedure

At first step, the DFTB [22-24] is based on the density functional theory of Hohenberg and Kohn in the formulation of Kohn and Sham. In addition, the Kohn-Sham orbitals ψ_i(r) of the system of interest are expanded in terms of atom-centered basis functions {φ_m(r)},

While so far the variational parameters have been the real-space grid representations of the pseudo wave functions, it will now be the set of coefficients c_im. Index m describes the atom, where Φ_m is centered and it is angular as well as radially dependent. The Φ_m is determined by self-consistent DFT calculations on isolated atoms using large Slater-type basis sets.

In calculating the orbital energies, we need the Hamilton matrix elements and the overlap matrix elements. The above formula gives the secular equations

Here, c_im’s are expansion coefficients, ∈_i is for the single-particle energies (or where ∈_i are the Kohn-Sham eigenvalues of the neutral), and the matrix elements of Hamiltonian H_mn and the overlap matrix elements S_mn are defined as

They depend on the atomic positions and on a well-guessed density ρ(r). By solving the Kohn-Sham equations in an effective one particle potential, the Hamiltonian  is defined as

To calculate the Hamiltonian matrix, the effective potential V_eff has to be approximated. Here,  being the kinetic-energy operator   and V_eff(r) being the effective Kohn-Sham potential, which is approximated as a simple superposition of the potentials of the neutral atoms,

V_j ⁰ is the Kohn-Sham potential of a neutral atom, r_j=r − R_j is an atomic position, and R_j being the coordinates of the j -th atom.

Finally, the short-range interactions can be approximated by simple pair potentials, and the total energy of the compound of interest relative to that of the isolated atoms is then written as:

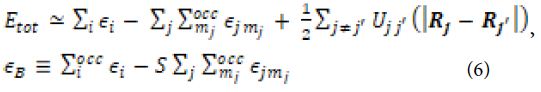
Here, the majority of the binding energy (∈_i) is contained in the difference between the single-particle energies ∈_i of the system of interest and the single-particle energies ∈_jmj  of the isolated atoms (atom index j, orbital index m_j), U_jj,(|R_j – R_j,|) is determined as the difference between ∈_B and ∈_B^SCF for diatomic molecules (with E^SCF being the total energy from parameter-free density-functional calculations). In the present study, only the 5d and 6s electrons of the gold atoms are explicitly included, whereas the rest are treated within a frozen-core approximation [25].

Structural Re-optimization Process

In our case, we have calculated the numerical first-order derivatives of the forces (F_iα, F_jβ) instead of the numerical-second-order derivatives of the total energy (E_tot). In principle, there is no difference, but numerically the approach of using the forces is more accurate.

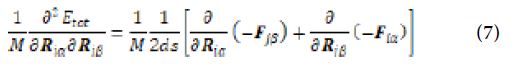
Here, F is a restoring forces which is acting upon the atoms, ds is a differentiation step-size and M represents the atomic mass, for homonuclear case. The complete list of these force constants (FCs) is called the Hessian H, which is a (3N x 3N) matrix. Here, i is the component of (x, y or z) of the force on the j’th atom, so we get 3N [26].

Results and Discussion

The Optimized Structure of the Clusters Au_{56, 57}

We present the vibrational spectrum analysis of the re-optimized Au_{56, 57} clusters, interestingly, all of them are having the very same point group symmetry C₁ at ground state, ∆E=0. Initially, the structures were found through a so-called genetic algorithm (GA) in combination with Density Functional Tight-Binding (DFTB) energy calculations and the steepest descent algorithm permitting a local total energy minimization. To sum up, we have accurately predicted the vibrational frequency of the clusters, and they are very strongly dependent on the size, structure, and shape of the clusters, mainly influenced by the stretching and the bending mode vibrations of the atoms that are due to changes on the bond length fluctuations for a small step-size ds=± 0.01 a.u. on the equilibrium coordinates [27]. By the way, for the perspective view of the structures, we have plotted with two different styles (Space-filling, Polyhedral).

The Vibrational Frequency (ω_i) Range of the Cluster Au₅₆ at ∆E=0

Table 1 shows the low (at the least) and the high (at the most) frequency range of the cluster Au₅₆, which occurs between 1.57 and 318.01 cm⁻¹, and the lowest energy geometrical structural view can be seen in Figure 1.

Table 1: The Normal modes (NVM) and the vibrational frequencies (ω_i) of Au₅₆ at ∆E=0

NVM (3N-6)	ωi [cm−1]	NVM (3N-6)	ωi [cm−1]	NVM (3N-6)	ωi [cm−1]
1	1.57	56	46.69	111	133.77
2	4.07	57	47.07	112	139.43
3	5.11	58	48.15	113	141.09
4	5.59	59	48.56	114	141.77
5	6.40	60	50.84	115	146.29
6	6.66	61	51.19	116	148.06
7	7.55	62	52.05	117	150.08
8	8.25	63	53.05	118	151.61
9	8.51	64	53.38	119	154.61
10	8.84	65	54.43	120	155.68
11	9.26	66	56.90	121	161.95
12	10.46	67	58.54	122	163.12
13	10.94	68	59.15	123	165.09
14	11.18	69	60.35	124	167.01
15	12.19	70	61.98	125	169.96
16	13.45	71	63.18	126	172.26
17	13.88	72	64.48	127	173.82
18	14.04	73	65.20	128	175.76
19	14.99	74	67.41	129	180.95
20	15.77	75	68.83	130	182.55
21	16.57	76	68.99	131	184.90
22	16.80	77	70.81	132	187.54
23	18.40	78	71.84	133	188.53
24	18.70	79	74.30	134	189.55
25	18.91	80	76.21	135	195.11
26	19.91	81	77.43	136	196.68
27	20.26	82	78.78	137	198.57
28	20.66	83	79.98	138	201.34
29	21.48	84	81.12	139	205.43
30	22.50	85	84.32	140	207.38
31	23.34	86	84.85	141	207.68
32	23.60	87	87.95	142	213.72
33	24.26	88	90.62	143	216.71
34	25.21	89	90.98	144	222.20
35	26.32	90	91.79	145	223.46
36	26.70	91	94.03	146	228.91
37	27.81	92	97.06	147	229.69
38	28.95	93	98.99	148	234.72
39	29.84	94	100.76	149	237.25
40	31.43	95	102.18	150	239.80
41	31.86	96	103.86	151	243.65
42	32.25	97	106.26	152	249.53
43	33.62	98	108.60	153	250.14
44	35.04	99	110.05	154	251.74
45	36.19	100	110.69	155	253.00
46	36.87	101	113.66	156	254.43
47	37.58	102	114.75	157	260.70
48	37.88	103	116.95	158	263.48
49	38.45	104	121.10	159	274.92
50	39.88	105	121.61	160	275.45
51	41.81	106	123.40	161	304.84
52	42.37	107	126.49	162	318.01
53	43.04	108	127.67	163	–
54	44.44	109	131.87	164	–
55	45.72	110	132.70	165	–

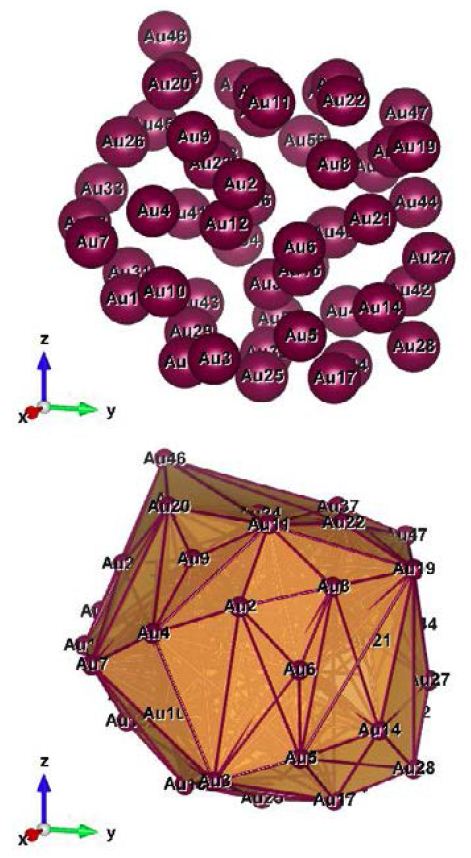
Figure 1: Au₅₆ (C₁); Style (Space-filling [left], Polyhedral [right]): The lowest energy geometrical structure of the Au₅₆ cluster. Standard orientation of crystal shape at ∆E = 0.

Firstly, the cluster has some low frequencies (ω_min) in between 1.57-9.26 cm⁻¹, which is only for the very first 11 NVM that comes even below the scale of Far Infrared FIR, IR-C 200-10 cm⁻¹. Secondly, for the 12-137 NVM, the frequency ranges occurred between 10.46-198.57 cm⁻¹, which comes within the range of Far Infrared FIR, IR-C 200- 10 cm⁻¹. Thirdly, the rest of the 138-162 NVM, is having the maximum high frequencies, which are ((ω_i) – 201.34-318.01 cm⁻¹) falling within the range of Mid Infrared MIR, IR-C 3330-200 cm⁻¹.

The Double and the Triple State Degeneracy (ω_i)

[{5.11, 5.59} {6.40, 6.66} {8.25, 8.51, 8.84} {10.46, 10.94} {13.45, 13.88} {14.04, 14.99} {16.57, 16.80} {18.40, 18.70, 18.91} {20.26, 20.66} {23.34, 23.60} {26.32, 26.70} {31.43, 31.86} {36.19, 36.87} {37.58, 37.88} {48.15, 48.56} {53.05, 53.38} {68.83, 68.99} {84.32, 84.85} {90.62, 90.98} {110.05, 110.69} {121.10, 121.61} {141.09, 141.77} and {207.38, 207.68}] in cm⁻¹_.

The Vibrational Frequency (ω_i) Range of the Cluster Au₅₇ at ∆E=0

Table 2 shows the low (at the least) and the high (at the most) frequency range of the cluster Au₅₇, which occurs between 2.59 and 336.04 cm⁻¹, and the lowest energy geometrical structural view can be seen in Figure 2.

Table 2: The Normal modes (NVM) and the vibrational frequencies (ω_i) of Au₅₇ at ∆E=0

NVM (3N-6)	ωi [cm−1]	NVM (3N-6)	ωi [cm−1]	NVM (3N-6)	ωi [cm−1]
1	2.59	56	50.09	111	131.98
2	3.90	57	50.76	112	134.76
3	5.69	58	51.17	113	137.88
4	6.03	59	51.99	114	141.31
5	6.51	60	53.73	115	142.46
6	7.44	61	54.53	116	143.49
7	7.91	62	55.92	117	144.62
8	9.58	63	57.10	118	148.21
9	10.10	64	57.55	119	152.57
10	10.83	65	58.41	120	154.79
11	11.59	66	58.58	121	156.54
12	12.22	67	59.94	122	158.23
13	12.51	68	61.18	123	160.74
14	13.12	69	62.43	124	163.87
15	13.45	70	63.48	125	165.20
16	14.47	71	63.78	126	168.35
17	14.72	72	65.35	127	171.29
18	15.66	73	67.23	128	173.69
19	17.24	74	68.31	129	175.53
20	17.47	75	69.97	130	178.67
21	18.23	76	71.74	131	181.40
22	20.28	77	73.09	132	181.74
23	21.02	78	73.48	133	185.41
24	21.75	79	73.54	134	186.96
25	22.61	80	74.43	135	189.75
26	23.11	81	77.77	136	193.58
27	24.08	82	79.01	137	198.70
28	24.89	83	80.06	138	199.87
29	25.40	84	80.64	139	201.61
30	25.97	85	81.86	140	203.43
31	26.66	86	83.96	141	204.74
32	27.64	87	85.31	142	209.70
33	28.48	88	88.12	143	212.31
34	29.36	89	90.19	144	215.27
35	30.02	90	93.79	145	218.89
36	30.67	91	93.99	146	219.13
37	32.91	92	96.01	147	227.32
38	33.34	93	98.95	148	229.48
39	33.86	94	99.17	149	237.44
40	35.36	95	101.53	150	239.56
41	35.73	96	103.34	151	243.69
42	36.41	97	103.88	152	246.65
43	37.67	98	107.90	153	249.68
44	38.15	99	109.27	154	251.20
45	39.10	100	110.30	155	257.30
46	40.65	101	111.69	156	261.52
47	41.97	102	115.40	157	263.64
48	42.76	103	116.45	158	266.55
49	43.24	104	117.87	159	269.54
50	43.63	105	120.11	160	273.32
51	44.45	106	121.17	161	274.25
52	45.15	107	122.44	162	282.04
53	45.62	108	126.24	163	287.47
54	47.84	109	129.91	164	288.58
55	49.21	110	131.47	165	336.04

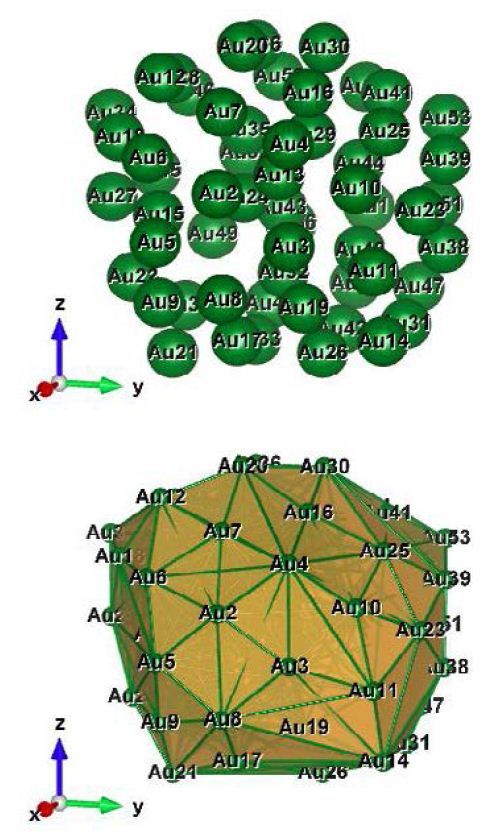
Figure 2: Au₅₇ (C₁); Style (Space-filling [left], Polyhedral [right]): The lowest energy geometrical structure of the Au₅₇ cluster. Standard orientation of crystal shape at ∆E = 0.

Firstly, the cluster has some low frequencies (ω_min) in between 2.59-9.58 cm⁻¹, which is only for the very first 8 NVM that comes even below the scale of Far Infrared FIR, IR-C 200-10 cm⁻¹. Secondly, for the 9-138 NVM, the frequency ranges occurred between 10.10-199.87 cm⁻¹, which comes within the range of Far Infrared FIR, IR-C 200- 10 cm⁻¹. Thirdly, the rest of the 139-165 NVM, is having the maximum high frequencies, which are ((ωi) – 201.61 – 336.04 cm⁻¹) falling within the range of Mid Infrared MIR, IR-C 3330-200 cm⁻¹.

The Double and the Triple State Degeneracy (ωi)

[{6.03 6.51} {7.44 7.91} {10.10 10.83} {12.22 12.51} {13.12 13.45} {14.47 14.72} {17.24 17.47} {21.02 21.75} {24.08 24.89} {25.40 25.97} {30.02 30.67} {33.34 33.86} {35.36 35.73} {43.24 43.63} {45.15 45.62} {50.09 50.76} {51.17 51.99} {57.10 57.55} {58.41 58.58} {63.48 63.78} {73.09 73.48 73.54} {80.06 80.64} {93.79 93.99} {103.34 103.88} {131.47 131.98} and {181.40 181.74}] in cm⁻¹.

It has occurred within the range of Far Infrared FIR, IR-C 200-10 cm⁻¹. Certainly, such kind of spectrum could be highly possible to observe in the experimental calculations, upon availability in the near future. In addition to that due to the degree of degeneracy [which is being composed by] that gives a deep interpretation about the elliptical motion () but could be multiple single motions.

Size and the Shape Effects

In Table 3, the third column shows the spectral ranges that have been influenced with respect to the size of the clusters, the shape of the structures, and the arrangement of the atoms (inner core, and the overall outer surface of the edges), as well as the short and the long-range interactions due to the inter-nuclear attraction and the repulsive energies.

Table 3: The double and the triple state degeneracy of the clusters, Au_{56, 57} at ∆E=0

Gold Nanoclusters (AuNCs)	Point Groups s(PG) Symmetry	Spectral Range (Min-to-Max) ωi [cm-1]	Double (D) & Triple (T) State Degeneracy [DT]{pairs}	Total Number of Pairs	Total Random Number (RN)  of Different States of Equal Energy RN=(D*pairs+T*pairs)	Predicted Spectral Range Only for D, T-Degeneracies. A: Far Infrared FIR, IR – C 200 – 10 cm-1 B: Mid Infrared MIR, IR – C 3330 – 200 cm–1 X: Lesser than both, A and B
Au56	C1	1.57-318.01	D21 T2	23	48	A, B, X
Au57	C1	2.59-336.04	D25 T1	26	53	A, X

Once again, we are first to present, the vibrational frequencies of bigger-sized clusters (Au_{56, 57}) and the shell-like structure (of course, they are part of the family of so-called full-shell clusters) at ∆E=0 by using the numerical finite-differentiation method with the DFTB approach. We have observed the vibrational spectrum, the minimum starting, and the maximal end ranges that vary between 1.57 cm⁻¹ and 336.04 cm⁻¹ at ∆E=0. Moreover, amazingly the occupancy of the multiple double and the triple state degeneracy is revealed on the gold atomic clusters, Au_{56, 57} (refer to Table 3). Interestingly, more number of the double-state degeneracy may depend on the nearest neighboring atoms, and their interactions, as well as the zig-zag circumstances of the outermost surface surrounded by them. We are able to see, a maximum, of 26 total double pairs have occurred on the Au₅₇ cluster.

Conclusions

We have observed the vibrational properties of the gold clusters in order to explore the stability and the structures. We have designed a mini formula for the occupancy of the double and the triple state degeneracy. Above all, we have pinpointed the correct location of the spectrum, through Far Infrared FIR, IR-C 200-10 cm^-1, and Mid Infrared MIR, IR-C 3330-200 cm^-1. In addition to that, our prediction will help the researchers to develop a range of potential applications such as catalysis, biomedicine, imaging, optics, and energy conversion.

Acknowledgements for Funding

Initially, the main part of this work was supported by the German Research Council (DFG) through project Sp 439/23-1. We gratefully acknowledge their very generous support.

References

1. Griffith WP (1967) The Chemistry of the Rarer Platinum Metals (Os, Ru, Ir, and Rh) Interscience Publishers.
2. Hartley FR (1973) The Chemistry of Platinum and Palladium: With Particular Reference to Complexes of the Elements. Applied Science Publishers Ltd.
3. Huang X (2016) Polymer Ligand Stabilized Fluorescent Platinum Nanoclusters: Synthesis, Characterization, and Their Applications.
4. Siegel RW (1994) Nanostructured materials -mind over matter. Nanostructured Materials 4: 121-138.
5. Huang X, Li Z, Yu Z, Deng X, Xin Y (2019) Recent Advances in the Synthesis, Properties, and Biological Applications of Platinum Nanoclusters. Journal of Nanomaterials.
6. Liangliang W, Weihai F, Xuebo C. (2016) The photoluminescence mechanism of ultra-small gold clusters. Chem. Chem. Phys. 18: 17320-17325.
7. Andres RP, Bein T, Dorogi M, Feng S, Henderson JI, et al. (1996) Coulomb Staircase at Room Temperature in a Self-Assembled Molecular Nanostructure. Science 272: 1323-1325. [crossref]
8. Young CC, Han ML, Woo YK, Kwon SK, Tashi N, et al. (2007) How Can We Make Stable Linear Monoatomic Chains? Gold-Cesium Binary Subnanowires as an Example of a Charge-Transfer-Driven Approach to Alloying, Rev.Lett. [crossref]
9. Li J, Liu Y, Zhang J, Liang X, Duan H (2016) Density functional theory study of the adsorption of hydrogen atoms on Cu2X (X=3d) clusters. Chem Phys Lett 651: 137-143.
10. Chuanchuan Z, Haiming D, Xin Lv, Biaobing C, Ablat A, et al. (2019) Static and dynamical isomerization of Cu38 cluster. Scientific Reports 9: 7564. [crossref]
11. Ignacio L, Garzon, Alvaro Posada-Amarillas (1996) Structural and vibrational analysis of amorphous Au55 clusters. Phys Rev B 54: 11796.
12. Bravo-Perez G, Garzon IL, Novaro O (1999) Ab initio study of small gold clusters. THEOCHEM 493: 225-231.
13. Bravo-Perez G, Garzon IL, Novaro O (1999) Non-additive effects in small gold clusters. Chem Phys Lett 313: 655-664.
14. Sauceda HE, Mongin D, Maioli P, Crut A, Vallee F, et al. (2012) Vibrational properties of metal nanoparticles: Atomistic simulation and comparison with time-resolved investigation. J Phys Chem C 116: 25147-25156.
15. Sauceda HE, Pelayo JJ, Salazar F, Perez LA, Garzon IL (2013) Vibrational spectrum, caloric curve, low-temperature heat capacity, and Debye temperature of sodium clusters: The Na139+case. J Phys Chem C 117: 11393-11398.
16. Sauceda HE, Salazar F, Perez LA, Garzon IL (2013) Size and shape dependence of the vibrational spectrum and low-temperature specific heat of Au nanoparticles. J Phys Chem C 117: 25160-25168.
17. Sauceda HE, Garzon IL (2015) Structural determination of metal nanoparticles from their vibrational (phonon) density of states. J Phys Chem C 119: 10876.
18. Dugan N, Erkoc S (2008) Phys Stat Sol B 245, 695.
19. Dong Y, Springborg M (2007) Global structure optimization study on Au2-20. Eur Phys J D 43: 15-18.
20. Warnke I (2007) Heat Capacities of Metal Clusters. Diploma Thesis (Research Assistant and Diploma Research), Saarland University.
21. Dvornikov M (2004) Formulae of numerical differentiation.
22. Porezag D, Frauenheim Th, Kohler Th, Seifert G, Kaschner R (1995) Construction of tight-binding-like potentials on the basis of density-functional theory: Application to carbon. Phys Rev B 51: 12947. [crossref]
23. Seifert G, Schmidt R (1992) Molecular dynamics and trajectory calculations: The application of an LCAO-LDA scheme for simulations of cluster-cluster collisions. New J Chem 16: 1145.
24. Seifert G, Porezag D, Th. Frauenheim (1996) Calculations of molecules, clusters, and solids with a simplified LCAO-DFT-LDA scheme. Int J Quantum Chem 58: 185-189.
25. Seifert G (2007) Tight-Binding Density Functional Theory: An Approximate Kohn-Sham DFT Scheme. J Phys Chem A 111: 5609-5613.
26. Press WH, Teukolsky SA, Vetterling WT, Flannery BP (2007) Numerical Recipes in Fortran. Cambridge University Press.
27. Vishwanathan K (2018) Bonding Forces and Energies on the Potential Energy Surface (PES) of the Optimized Gold Atomic Clusters by a Differentiation Step-Size (ds=±0.01 a.u.) via DFTB Method. Nanosci Technol 5: 1-4.