Introduction
The first purpose of the present paper is to clarify the scientific approach Einstein [1] adopted when he developed the Specia Relativity Theory (→SRT). This can be done when we compare his approach with two long-established and characteristically different methods in use to gain relevant scientific knowledge: the phenomenological and the axiomatic method.
The second aim of this paper will then be to analyse from an immanent-logical point of view:
(i) Einstein’s postulates of the SRT and their implications;
(ii) How Einstein – starting from the postulates he had introduced – attempted to derivate the Lorentz [2] Transformations.
Said in other terms: I shall concentrate my attention on the inner consistency of the SRT.
Two Classical Methods for Scientific Knowledge
The Phenomenological Approach
(i) We often start our observations and investigations with appearances of sensory modality. Consider, for instance, the following experiences (1. – 6.): 1. We look at the sun, the moon, the planets, and unexpectedly begin to wonder about their respective movements; 2. We perceive several flowers, and suddenly set on to wonder what traits they may have in common and wherein they could differ from each other – and this sets in motion a closer look at them and a comparison of their striking structures; 3. We gaze at several birds, and suddenly find ourselves engaged in observing and comparing their behaviour; 4. We look at tides and sea currents and begin to wonder about the rhythms they are involved in; 5. We investigate the phenomena of electromagnetic induction – and go over to arrange an experimental setting, varying it in the course of our observations, etc.
(ii) Many of the investigations hinted at set off from “open” intentions, which we specify when intending to clarify the relations implicit in the phenomena that puzzle us.
(iii) We are thus led to the formulation of rules, tendencies, laws; we become aware of certain probabilities – and are thereby encouraged to modify our primordial intention, to ask new questions, to foster new investigations, always endeavouring to remain close to the phenomena, saving the appearances.
The Axiomatic Approach
First systematically presented by Euclid [3,4] in his Elements of Geometry, further developed and specified by logicians and mathematicians (e.g. B. Pascal [5], G. Frege [6-8], P. Finsler [9]) in the course of 2000 years, the characteristic features of an axiomatic approach can be summarized as follows:
(i) If we aim to open a field of knowledge according to the axiomatic method, we start from a cognitive intention which we specify step by step, formulating clear postulates. We thereby establish what kind of mental processes we intend to be engaged in.
(ii) We will then set forth to introduce certain words, signs, terms, defining unambiguously what these expressions shall henceforth mean and refer to within the context at issue.
(iii) Constitutive to the axiomatic method is the fact that if we steadily hold to the postulates we are led to elementary, fundamental insights, i.e. axioms. Epistemologically speaking, the axioms follow necessarily from the postulates. They are basic insights which cannot be reduced to yet more fundamental assertions. We can therefore look upon the axioms as being self-evident.
(iv) Starting from the axioms, we can derive higher structured propositions, i.e. theorems, by means of logical reasoning. This holds true, even if many a researcher may catch sight of the content of a theorem, before realizing that the theorem in question can be logically traced back to the axioms.
(v) If we develop an axiomatic system, we implicitly acknowledge that the Principles of Logic are unrestrictedly valid – at all levels of our investigation. The two main principles I’ll be concerned with in the present paper are: a) The Principle of Identity, requiring that every term we have introduced maintain its univocal meaning throughout the entire investigation; b) The Principle of Non-Contradiction, demanding that neither postulates nor axioms (and, consequently, theorems) contradict one another.
(vi) Accordingly, in fields of knowledge opened and determined by the axiomatic method (e.g. in pure mathematics), a mental item (a “thing”) exists, and an assertion is true if the former and the latter are exempt from contradictions.
A Short Comparison of the Two Approaches to Scientific Knowledge Reveals
(i) A scientist working phenomenologically does not a priori question the reality of the objects and appearances he deals with in his investigations; he simply tries to unveil the rules and correlations hidden in them.
(ii) A mathematician embracing the axiomatic method formulates postulates of exclusively mental content, advancing to axioms and theorems. The existence of the objects he is concerned with, as well as the truth of his findings, depends entirely on the non-contradiction of the postulates – and this includes the axioms and the theorems that correspond to the postulates. A mathematician has the right to declare that certain signs, ciphers, symbols, drawn figures represent the mental objects he conceives and deals with, but the signs and symbols lack value of their own – they rather are a mnemonic that helps us to pursue the line of thought expressed in the postulates and axioms of purely mental content.
(iii) Although the phenomenological and the axiomatic approaches differ from one another, each one of them is clearly determined, and both are – in principle – free from contradictions.
Dogmatic-deducible Approaches to Scientific Cognition
A third, completely different approach to achieve scientific cognition is practised by researchers who, imitating mathematicians, introduce postulates, but extend their enunciations to include elements which essentially belong to the modalities of the world of sensory perceptions. In other words: their postulates are not restricted to purely mental categories which – as a mere aid for grasping their content – can be illustrated by diagrams, figures, symbols; on the contrary, the postulates we are now talking about – which, as I said, include elements belonging to the world of sensory perceptions – prescribe how these latter elements must appear and evolve according to the postulates. These do not hint at tentative models, meant to explain certain phenomena – they are strict, rigid prescriptions of the sensory modalities to be expected under clearly defined settings.
I call such an approach a dogmatic-deducible theory. A good example of such theory (or approach) is Einstein’s introduction to his Special Relativity Theory (=SRT) in the papers of 1905 and 1922/56.
The Special Relativity Theory (SRT) – A Dogmatic-Deducible Theory
Einstein based his SRT on two explicit postulates:
Postulate 1: The Postulate of Relativity (=PoR), demanding that in two inertial frames of reference K° and K’, moving reciprocally at a constant speed v along their parallel x°- and x’-axes, identical laws of Nature are valid;
Postulate 2: The Postulate of Constant Speed of Light (=PoL), originally introduced by declaring that for observers firmly placed along the x°-axis of K°, a flash of light L°, emitted by a source of light Q° of K° in the positive direction of the x°-axis, will always be propagated and arrive at an equal speed c, independently of any motion of Q° along the x°-axis at the time it emits L°.
I shall call this arrangement: Configuration I.
I have formulated both postulates of the SRT in a clear, unambiguous way – in complete accord with the formulations advanced by Einstein in his papers of 1905 and 1922/56.
The postulates reveal that each one of them contains several elements that do not belong to the realm of the purely mental concepts of mathematics and logic:
(i) In Postulate 1, the PoR, we find “frames of reference that are moving reciprocally at a constant speed v”; and also “laws of Nature”;
(ii) In Postulate 2, the PoL, we have “a flash of light will always be propagated and arrive at an equal speed c, independently of any motion of Q° along the x°-axis at the time it emits L° “.
Such terms as ‘speed’, ‘motion’, ‘flash’, ‘Laws of Nature’ form an essential part of what is demanded in the Einsteinian Postulates. These postulates demand and determine how certain elements of sensory perceptive modality must appear and have to evolve within the system presented and specified by the PoR and the PoL. They strictly prescribe what an observer in K° and K’ must observe and measure.
Let us now look at Configuration I, as introduced by Einstein: (Figure 1).
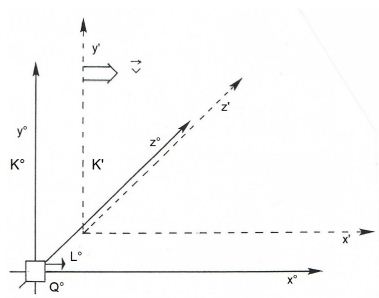
Figure 1: K°, K’: frames of reference (inertial systems); v: relative speed of K’ with respect to K°; Q°: source of light, placed at the zero point of the coordinates of K°, which emits the flash of light L° in the positive direction of the x°-axis. The figure represents Configuration I.
Let us now change to Configuration II: (Figure 2).
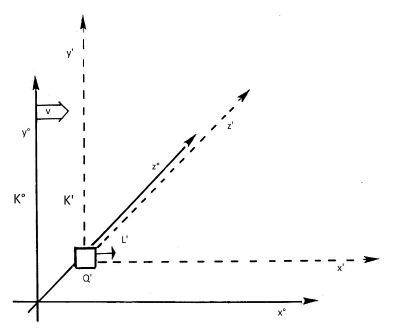
Figure 2: K’, K°: frames of reference (inertial systems); v: relative speed of K° with respect to K’; Q’: source of light, placed at the zero point of the coordinates of K’, which emits the flash of light L’ in the positive direction of the x’-axis. The figure represents Configuration II.
If we compare Configuration II with Configuration I, we see that the two configurations are completely symmetrical. One of the most important points to consider is, that the PoR has been applied correctly: The source of light Q°, placed at the zero point of the coordinates of K° in Configuration I, has been replaced by the source of light Q’, correctly situated at the zero point of the coordinates of K’. And, of course, whereas in Configuration I it was stipulated, that the flash of light L° would move with velocity c with respect to observers firmly placed on the positive x°-axis of K°, independently of any motion of Q° in relation to these observers of K° – we now see that in Configuration II we have established completely symmetric conditions, resulting in an enunciation that proclaims that the flash of light L’, emitted by Q’ in the positive direction of the x’-axis will move with the same velocity c with respect to observers of K’ that are firmly located on the x’-axis, independently of any motion of Q’ at the time it emits L’. If we transform Configuration I into Configuration II taking care to install completely symmetric conditions, the result is totally free from contradictions.
Einstein’s Logic Fallacies in His Papers of 1905 and 1922/56:
The Lack of Symmetric Conditions
Einstein wrote that the flash of light L° in K° in Configuration I moves with constant speed c for all observers firmly placed in K° and would “… in connection with the Principle of Relativity [i.e. PoR] also [propagate] with velocity V [i.e. c] when measured in the moving system [i.e. K’]”… In other words: also move with the same speed c for observers firmly placed on the x’-axis of K’. In short: Einstein argued that the same light-signal L°, emitted by the source of light Q° of K° and moving at speed c for observers at rest in K°, would also propagate itself for observers at rest in K’ at equal speed c, notwithstanding the premise that the systems K° and K’ were moving in relation to each other at the constant speed v. Einstein erroneously applied the PoR together with the PoL directly to the flash of light L°, without transferring the source of light from K° to K’. He didn’t arrange for K’ a configuration symmetric to the one he had established for K°. This lack of symmetry between K° and K’ definitely rules out any application of the PoR. By neglecting to introduce strictly symmetric configurations in K’ to those in K°, Einstein violated the Principle of Non-Contradiction – since K’ is, in his case, no longer equivalent to K°, although he had begun with the premise that the conditions were to be equivalent.
The Mutual Relative Speed of K° and K’
Besides the lack of symmetry, there is yet another point worth looking at: Einstein established as a premise that the mutual relative speed of K° and K’ is to be v ≠ 0, when measured by observers in K°, and also when measured by observers in K’. This implies that exactly the same units of measurement are to be valid in K° and in K’. By strictly holding to this premise, it follows that the flash of light L°, emitted by Q° in K° cannot move at same speed c for observers at rest in K’ as for observers at rest in K°. If the mutual relative velocity between K° and K’ remains v ≠ 0 – with the same value, when determined by observers in K’ and in K°-, the flash of light L° can only move artificially with the same numerical value c for observers in K’ as in K°, if we deliberately change the units of measurement in K’ in a way that the same numerical value issues. But by acting in such a way and implicitly – and tacitly – maintaining the very same symbols ‘m’ for meters and ‘s’ for seconds in K’, as well as in K°, we convey different meanings to these symbols in K’ with respect to the meaning they have in K°- and this is an obvious transgression of the Principle of Identity.
Conclusion
Einstein’s 1905 and 1922/56 papers on the introduction of his Special Relativity Theory are logically inconsistent. Einstein misapplied the Postulate of Relativity, since he neglected to establish symmetric conditions in the equivalent frames of reference K° an K’ he had introduced at the outset of his papers. Furthermore, Einstein transgressed the Principle of Identity, since he maintained the same symbols for length and time throughout his papers, but changed their meaning, i.e. what they referred to at the beginning. Finally, Einstein maintained that the same units of measurement were to be valid in both systems K° and K’ as far as the determination of their mutual relative velocity was concerned, but untenably changed the units with regard to the determination of the speed of a light-flash in the two systems he considered. It follows that Einstein’s Special Relativity Theory is inconsistent. It violates the Principle of Identity and the Principle of Non-Contradiction. As such, the SRT cannot be corroborated experimentally. Experimental findings have to be interpreted on a consistent line of thought.
References
- Einstein A (1969) Grundzüge der Relativitätstheorie. Springer.
- Lorentz HA, Einstein A,Minkowski H (1974) Das Relativitätsprinzip. Eine Sammlung von Abhandlungen. Darmstadt: Wissenschaftliche Buchgesellschaft.
- Euclides (1791) The Elements of Euclid. London, Wingrove.
- Euclides (1814-1818) Les Oeuvres d’Euclid, en grec, latin et en français. T : 1-3
- Pascal B(1986) L’esprit de la géométrie. De l’art de persuader.
- Frege G (1961) Die Grundlagen der Arithmetik. Eine logisch-mathematische Untersuchung über den Begriff der Zahl. Darmstadt: Wissenschaftliche Buchgesellschaft.
- Frege G (1967) Kleine Schriften, herausgegeben von I. Angelelli. Darmstadt: Wissenschaftliche Buchgesellschaft.
- Frege G (1969) Nachgelassene Schriften, herausgegeben von H. Hermes, F. Kambartel, F. Kaulbach. Hamburg: Meiner.
- Finsler P (1966) Finsler Set Theory: Platonism and Circularity.