DOI: 10.31038/CST.2018343

Abstract

Purpose

To develop a general course of action for oxygen distribution calculations, in macroscopic tumours, using Graphics Processing Units (GPU) for parallel computation.

Methods

A vessel tree structure and an associated macroscopic (about 100 g) tumour were generated, using a stochastic method and Bresenham’s line algorithm. The vessel dimensions were adjusted to correspond to measured values and each vessel voxel was assigned an oxygen value, based on its distance from an incoming large vessel. Diffusion and consumption were modelled using a Green’s function approach together with Michaelis-Menten kinetics. The tumour was inscribed in a matrix of 10¹² elements. The computations were performed using a parallel method (CUDA), where the tumour was sectioned into about 18000 sub-matrices, overlapping to avoid edge effects, which were processed individually by three GPU: s. The result matrices were cropped to original size to enable concatenation.

Results

The entire process took approximately 48 hours, corresponding to 20 seconds per sub-matrix, which is more than fifty times faster when compared to the equivalent CPU calculation. Sample images illustrate the oxygen distribution of our poorly vascularised example tumour.

Conclusions

Regardless of the model accuracy and performance, the improvement in computation time using GPU calculations is highly advantageous. The preferred, parallel calculation method lowers the computation time by over 98% in this example, while maintaining full quality of performance. This is a remarkable improvement, which makes it possible to test and develop relevant models significantly faster. This computation approach does not depend on how the tumour model was created, nor is it limited to the type of model used here, but may be applied to a variety of problems, involving element-wise operations on large matrices.

Keywords

Parallel Computing, Modelling, Hypoxia, Radiosensitivity

Introduction

Numerical approaches to diffusion-consumption problems are frequently used for estimating tumour tissue oxygen transport [1–5]. When used in combination with oxygen consumption calculations, using for example the Michaelis-Menten model [6], they can provide valuable information on the characteristics of tumour oxygenation. However, there are limitations due to the extensive calculations and required computer memory. Provided sufficient accuracy, the computation times depend basically on volume and resolution. In practice, this limits decent computers to downsized experiments. This is unfortunate, since some oxygenation related effects need to be studied on clinically relevant tumour volumes in order to be properly evaluated. As we have established in previous studies, simplified calculations, e.g. through collapsing dimensions, and sub-sampling, rarely generate adequate results [5, 7].

In the previous studies we investigated the accuracy of two different approximative methods aiming to give a fast, detailed estimation of the oxygenation in a large tumour [7]. With the first method, the Individual Tree Method (ITM), we calculated the oxygen contribution from each microvessel tree in the tumour vasculature individually, down sampling the results to 100 µm cubical voxels and superposing them according to the entire vasculature. In the second method, the combined tree method, the distribution including all microvessel trees simultaneously in a 10 µm voxel model was calculated, but only for five randomly selected sample volumes of the entire tumour model. The conclusion, however, was that neither ITM nor CTM, applied to tumour samples, was sufficient to describe the oxygen status of the tumour, but that highly resolved calculations must be applied to the whole tumour. In this study, we attempt to find a way to perform such calculations and bypass the above limitations, performing parallel computations on graphical processing units (GPU) using CUDA®.

Methods

A macrovessel tree was generated, using the same method and parameter values as in Lagerlöf et al 2016. A total of 100 microvessel trees were generated accordingly and randomly assigned to each of the leaf nodes of the macrovessel tree. The combined vessel tree defines the irregularly shaped tumour, with a total volume of 100 cm³ used in these calculations. The microvessel voxels were assigned pO₂-values, depending on distance from the origin of the microvessel tree, ranging from 100 to 40 mmHg [7].

The smallest cuboid volume span by the vessels measured 9 × 10 × 11 cm³, approximately 10¹² voxels, side 10 µm. The calculations were made using a Gaussian diffusion kernel (equation 1) [8,9] for repeated convolution with the oxygen distribution matrix in time steps of
100 ms.

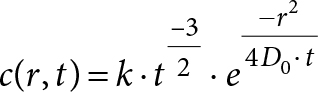(1)

The Michaelis-Menten model (Equation 2) was used to model concentration dependent oxygen consumption at every time step.

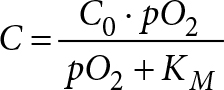(2)

In total, this required four single precision floating point number arrays (using 4 bytes of memory per element), holding vessel information, current oxygenation, oxygen consumption and the calculation result. For faster calculations, also the fourier transform of the oxygenation and of the diffusion kernel are needed, since convolution in the spatial domain is equivalent to multiplication in the frequency domain and the latter operation is faster for large matrices [8]. This would, in turn, require 6 · 4 · 10¹² bytes (21.8 TB) of available memory, which corresponds to 700 well equipped workstations. Therefore, sectioning the tumour matrix into sub-matrices was inevitable.

A large number of fairly simple, independent, matrix operations like these are well suited for performing on the computers (GPU). For this purpose, we used a computer equipped with three CUDA-compatible Nvidia titan X (gaming) GPUs. For optimum performance on the GPU, the preferred matrix size was 512 × 512 × 512, corresponding to 512 MB of data. With the purpose of limiting the edge effects of the convolutions to below 1%, each matrix needed 70 voxels of padding in all directions. This was achieved by overlapping the sub-matrices in the sectioning, leaving 372 × 372 × 372 voxels of valid data per sub-matrix, requiring a total of 18720 sub-matrices, of which 10156 were outside the actual tumour, therefore containing no oxygen or vessel data and thus were omitted from the calculations, leaving 8564 tumour sub-matrices. The sub-matrices were indexed to preserve the geometrical information of the original matrix.

Each of the matrices was passed to the first available GPU, along with the fourier transform of the 100ms oxygen diffusion kernel. On the GPU, the current oxygen distribution (at first iteration equal to vessel oxygen content) was fourier transformed and multiplied with the fourier transformed kernel. The resulting matrix was inversely transformed, the voxel-wise oxygen consumption was calculated (according to equation 2) and subtracted; the vessel oxygen data was restored. The process was repeated 300 times and the resulting matrices were returned to the CPU, where the padded edges were trimmed, an oxygen histogram was calculated and the data was saved to file. For quality assurance, the result of an individual sub-matrix calculation was compared voxel-wise to the equivalent CPU-calculation.

The indexing of the sub-matrices allows for any slice or (sufficiently small) sub-volume of the tumour to be easily loaded into the computer memory, for further calculation, visualisation or analysis.

Results

The entire process took approximately 48 hours, corresponding to 20 seconds per sub-matrix. When performed on an Intel® Core™ i7 CPU @ 2,7 GHz (representing normal conditions), the corresponding calculations would endure approximately four months (based on slightly over 20 minutes per sub-matrix in the comparative test calculations), providing the exact same result.

By this new simulation strategy of running the computations in parallel on GPUs detailed information about the oxygen level can be visualised and quantified. Figure 1 a-c shows the oxygenation in a central slice of the tumour in the x, y and z direction respectively. Irregular oxygen distributions are observed, and the oxygen level range from approximately 0 to 80 mmHg. Figure 2 illustrates the oxygen distribution in a 400 megavoxel sample in the centre of the tumour. Demonstrating the large variation in oxygen pressure within the tumour centre. A high fraction of the cells in this region will have a low oxygen pressure, which is non-beneficial for treatment strategies as radiation therapy.

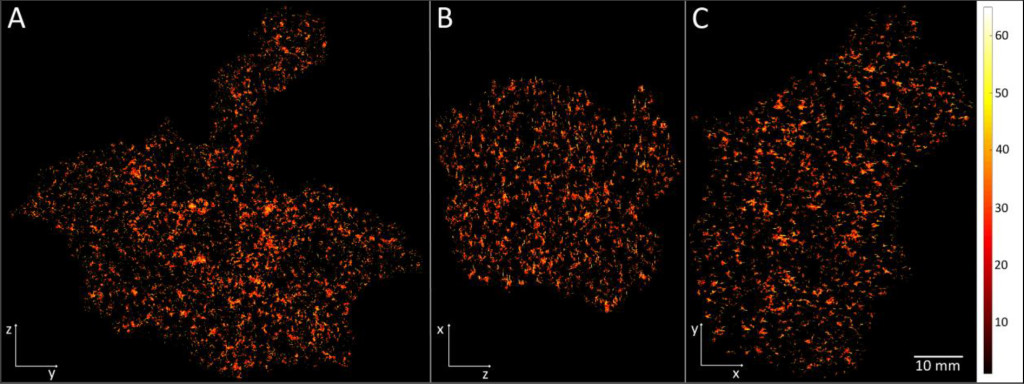
Figure 1. Illustration of the simulated oxygen distribution in the tumour centre slices in x (A), y (B) and z (C) direction. The colour bar shows the oxygen level from 0 to 65 mmHg. The white length scale is 10 mm.

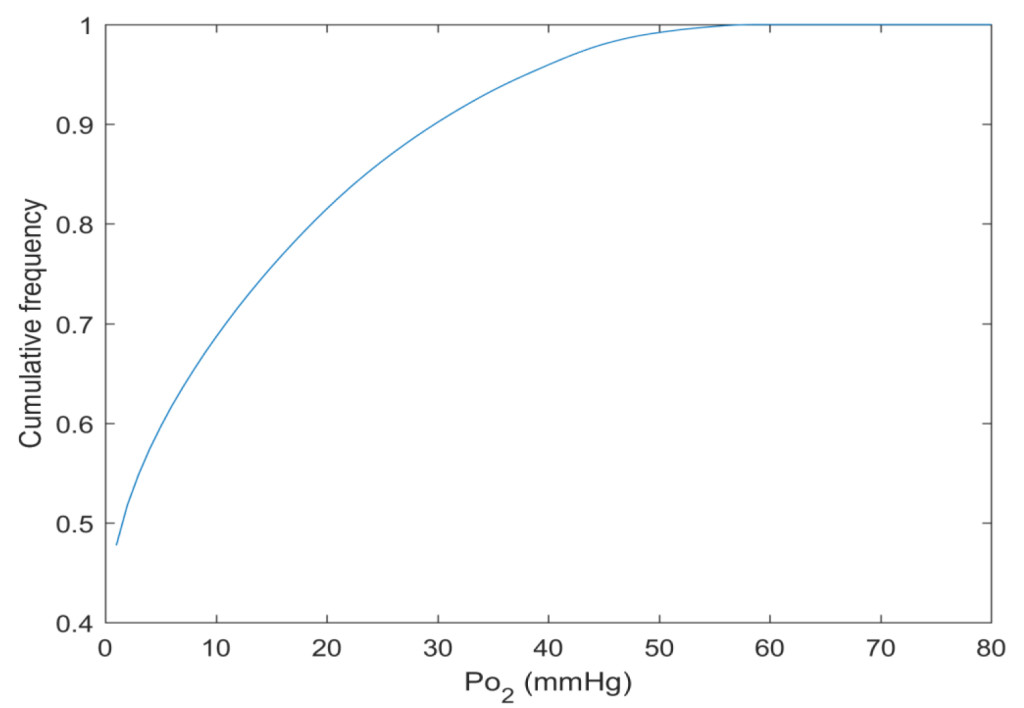
Figure 2. The cumulative oxygen distribution in a 400 megavoxel sample in the tumour centre.

Discussion

Regardless of the model accuracy and performance, the improvement in computation time using GPU calculations is highly advantageous. The preferred, parallel calculation method lowers the computation time by over 98% in this example, while maintaining full quality of performance. This is a remarkable improvement, which makes it possible to test and develop relevant models significantly faster. This computation approach does not depend on how the tumour model was created, nor is it limited to the type of model used here, but may be applied to a variety of problems, involving element-wise operations on large matrices and it only requires one standard workstation with GPU:s.

There is room for further progress though. Using state of the art equipment (newest NVIDIA Tesla GPUs dedicated for computation) there is roughly a speed gain of 6 compared to the GPUs used in this study [10]. Increasing the number of GPU:s to the maximum (8) gives another 2.7, which means that the calculation times may be reduced by approximately 16 times compared to what is presented here, which theoretically gives a total computation time of about three hours, 99.9 % faster than the estimated 120 days in our CPU comparison.

In addition, these GPUs are able to perform two arithmetic operations at the same time (under certain conditions), on half precision floating-point numbers. Lowering the precision to 16 bit also allows for twice the amount of data to be passed to the GPU per unit time, which means that the efficiency would increase by up to 4 and the computation time ideally could become as short as 45 minutes, a reduction by 99.97 %. However, this could possibly introduce rounding errors (depending on the numerical values used in the model) due to lowered precision. The results therefore would have to be validated. At these rates, the over-head times (data transfer between CPU, GPU and data storage) could become an issue, which makes it hard to estimate the actual time gain. In the event of lost performance due to this, the CPU may be bypassed and data transferred directly to and from GPU memory [11].

Finally, the maximum data transfer rates (8564 · 512 · 512 · 512 · 16/8 Bytes per 45 minutes) would exceed even the theoretical limitations of Superspeed+ (USB 3.1 gen 2 of 0.6 GB/s) as well as of conventional hard drives. Therefore, for convenient writing and reading of data to and from file, using current technology, a solid state drive (SSD) and an interface with sufficient throughput (PCI express or Thunderbolt 3), or at least two SSD:s (if Superspeed+, SATA III or Serial attached SCSI interface is preferred), are advised [12–15].

However, performance is continually improving and within a near future we can expect computation times to further decrease considerably, making this field of tumour modelling research even more exciting. The major initial advantage of faster computations is that it accelerates the evolution of realistic models due to a notable decrease in development cycle time. By extension it enables more accurate calculations to be performed faster, perhaps essentially in real time in clinical settings, for instance diagnostic imaging.

References

1. Harting C, Peschke P, Borkenstein K, Karger CP (2007) Single-cell-based computer simulation of the oxygen-dependent tumour response to irradiation. Phys Med Biol 52: 4775–4789. [crossref]
2. Adhikarla V, Jeraj R (2012) An imaging-based stochastic model for simulation of tumour vasculature. Phys Med Biol 57: 6103–6124. [crossref]
3. Dasu A, Toma-Dasu I, Karlsson M (2003) Theoretical simulation of tumour oxygenation and results from acute and chronic hypoxia. Physics in medicine and biology 48: 2829–2842.
4. Lagerlöf JH, Kindblom J, Cortez E, Pietras K, Bernhardt P (2013) Image-based 3D modeling study of the influence of vessel density and blood hemoglobin concentration on tumor oxygenation and response to irradiation. Medical physics 40: 024101.
5. Lagerlof JH, Kindblom J, Bernhardt P (2014) The impact of including spatially longitudinal heterogeneities of vessel oxygen content and vascular fraction in 3D tumor oxygenation models on predicted radiation sensitivity. Med Phys 41: 044101.
6. Secomb TW, Hsu R, Dewhirst MW, Klitzman B, Gross JF (1993) Analysis of oxygen transport to tumor tissue by microvascular networks. International journal of radiation oncology, biology, physics 25: 481–489.
7. Lagerlof JH, Bernhardt P (2016) Oxygen Distributions—Evaluation of Computational Methods, Using a Stochastic Model for Large Tumour Vasculature, to Elucidate the Importance of Considering a Complete Vascular Network. PloS one 11: 0166251.
8. ter Haar Romeny BM (2003) The Gaussian kernel,” Front-End Vision and Multi-Scale Image Analysis: Multi-Scale Computer Vision Theory and Applications. written in Mathematics 37–51.
9. Lagerlöf J, Diss Göteborg Göteborgs universitet (2014) Department of Radiation Physics, Institute of Clincial Sciences, The Sahlgrenska Academy, University of Gothenburg, Sweden.
10. WHAT IS GPU-ACCELERATED COMPUTING?, http://www.nvidia.com/object/what-is-gpu-computing.html
11. NVIDIA GPUDirect., https://developer.nvidia.com/gpudirect
12. Superspeed USB., http://www.usb.org/developers/ssusb
13. Thunderbolt 3 tehology brief.,
    https://thunderbolttechnology.net/sites/default/files/HBD16235_Thunderbolt_TB_r05.pdf
14. SATA-IO Releases SATA Revision 3.0 Specification.,
    https://sata-io.org/sites/default/files/documents/SATA-Revision-3.0-Press-Release-FINAL-052609.pdf
15. Serial Attached SCSI Technology Roadmap.,
    http://www.scsita.org/content/library/serial_attached_scsi_technology_roadmap/